Rapports harmoniques
C'était dans les années du baby-boom. Le pont-aux-ânes de la géométrie en classe de seconde était de déterminer le lieu des points M du plan tels que, pour deux points fixes A et B donnés, le rapport MA / MB est constant, égal à k. En ces temps reculés, les examinateurs sadiques posaient cette question à l'oral du premier bac, garante d'une inévitable catastrophe. Bien sûr, on trouve analytiquement l'équation du lieu : MA2 = k 2MB2. Pour les points A(, 0) et B(
, 0), on obtient, après développement, un cercle centré sur la droite (AB) en
et de rayon
.
Descartes aurait certainement été satisfait, mais pas les tenants de la géométrie synthétique.
À cette époque de la géométrie reine, on démontrait d'abord que les bissectrices au sommet M du triangle MAB interceptaient le côté opposé aux points I et J tels que IA / IB = JA / JB = k. En traçant la parallèle au côté [AM] en B, il suffit alors d'appliquer le théorème de Thalès aux triangles AIM et BII' et aux triangles AJM et BJJ'.
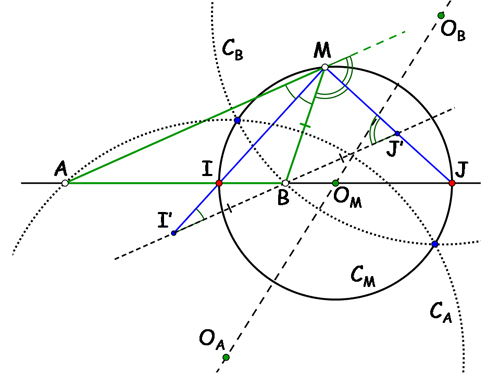
Les bissectrices étant perpendiculaires, le lieu cherché est donc le cercle CM de diamètre [IJ]. La division harmonique [A, B, I, J] rend harmonique le faisceau des droites (MA), (MI), (MB), (MJ), mais cela n'était pas pris en compte dans cette démonstration.
Le cercle CM, lieu du point M pour k fixé, est dit cercle d'Apollonius. On construit de même les cercles CA et CB avec les bissectrices aux sommets A et B. Ces trois cercles ont une corde en commun et leurs centres sont alignés sur la droite de Lemoine. De multiples propriétés illustrent ainsi l'esprit géométrique des mathématiciens de la fin du XIXe siècle, tels les Henri Brocard, Émile Lemoine et autres Joseph Neuberg.
Le flux des bornes
Le champ électrique créé par un fil rectiligne infini de charge linéique λ est radial, pour des raisons de symétrie, et de module
pour un point situé à la distance r du fil. Le potentiel V associé a pour expression
puisque le champ électrique dérive de son potentiel. Si le point M se déplace sur une équipotentielle, on a
.
La ligne de champ, qui porte le champ , est donc orthogonale à la ligne équipotentielle.
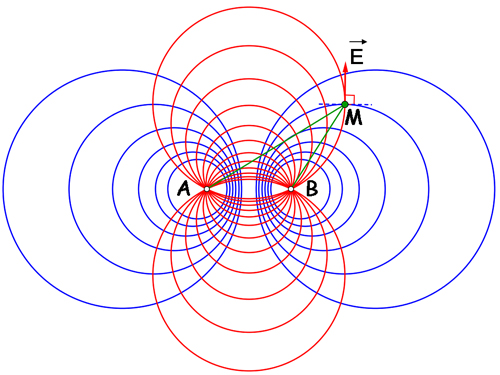
Si l'on considère deux fils perpendiculaires à un même plan, en A et B, et de charges linéiques opposées, le potentiel est proportionnel à la quantité ln(r2 / r1 ) en un point M du plan situé respectivement aux distances r2 et r1 des fils.
Les équipotentielles seront donc les courbes telles que r2 / r1 est constant. C'est la définition bipolaire des cercles d'Apollonius, qui constituent un faisceau admettant la médiatrice de [AB] pour axe radical (courbes bleues). Les lignes de champ sont les trajectoires orthogonales (courbes rouges) de ce faisceau : ce sont des cercles passant par A et B et de centre situé sur la médiatrice de [AB].
L'ensemble de ces lignes constitue un système de coordonnées orthogonales paramétré par α et β : dans un repère ayant pour axe des abscisses la droite (AB), et sa médiatrice pour axe des ordonnées,
et
où est la demi-distance de A à B.
Pour constant, on trouve les cercles bleus, de centre (
cot(
), 0) et de rayon
et pour β constant, le faisceau conjugué, d'axe radical l'axe des ordonnées, constitué des cercles (rouge) de centre (0, coth(
)) et de rayon
.
Si les densités linéiques sont de même signe, les lignes équipotentielles sont telles que le produit r1r2 est constant.
Ce sont des ovales de Cassini, dont les courbes orthogonales sont des hyperboles équilatères.