
Les coefficients binomiaux, omniprésents dans les mathématiques et en particulier en combinatoire et en probabilités, sont définis par
où k et n sont deux entiers tels que 0 ≤ k ≤ n.
La construction du triangle de Pascal utilise la propriété suivante :
Autrement dit, si les lignes et les colonnes sont numérotées de 0 à n, le coefficient de la ligne n + 1 et de la colonne k + 1 est égal à la somme du coefficient de la ligne du dessus (ligne n, colonne k + 1) et du coefficient précédent (ligne n, colonne k). Ces coefficients sont utilisés dans des domaines variés. Par exemple, pour développer (x + y)n en utilisant la formule du binôme de Newton, pour calculer des probabilités associées à une variable aléatoire qui suit une loi binomiale, pour déterminer les polynômes de Bernstein qui servent à construire les courbes de Bézier… Le triangle de Pascal peut même être utilisé en analyse quand on travaille avec des fonctions faisant intervenir une puissance, comme par exemple t ?2n-1 (cost)n où n est un entier naturel. De telles fonctions, périodiques et intégrables, peuvent être vues comme des signaux (sons, vidéos, etc.), que l'on peut donc manipuler comme tels en vue d'applications diverses : compression ou transmission d'information…
Une étape incontournable dans ces applications est alors de calculer la transformée de Fourier du signal. Si f est une fonction intégrable sur , on appelle transformée de Fourier de f la fonction
Cette opération permet de passer d'une fonction intégrable vue comme un signal à une autre fonction qui décrit des caractéristiques physiques de ce signal (amplitude, phase, fréquence du signal).
Les bienfaits du calcul formel
Tous les calculs seront réalisés avec la calculatrice formelle fx-CP400+E*. Cette dernière est en effet dotée d'un système de calcul formel (Computer Algebra System, ou CAS, en anglais) qui lui permet de faire des calculs symboliques, par exemple x + x = 2x, sans avoir donné de valeur à x.
La calculatrice formelle fx-CP400+E va nous faciliter la tâche puisque l'on pourra tout d'abord exécuter un programme qui dépend de n, puis calculer la transformée de Fourier des fonctions t ?2n-1 (cost)n, et enfin évaluer des sommes allant jusqu'à l'entier n. Et tout cela pour plusieurs valeurs de n, en écrivant de manière naturelle, sans avoir besoin de réécrire les calculs à chaque étape. L'élévation à la puissance n dans l'expression de la fonction permettra, en écrivant cos t sous la forme (ei t + e–i t) / 2, de faire naturellement intervenir les coefficients du binôme.
Commençons par construire un programme qui génère les n premières lignes du triangle de Pascal. Aller dans le menu Programme  .
.
Créer le programme ci-dessous en appuyant sur Edit puis sur Nouveau fichier.
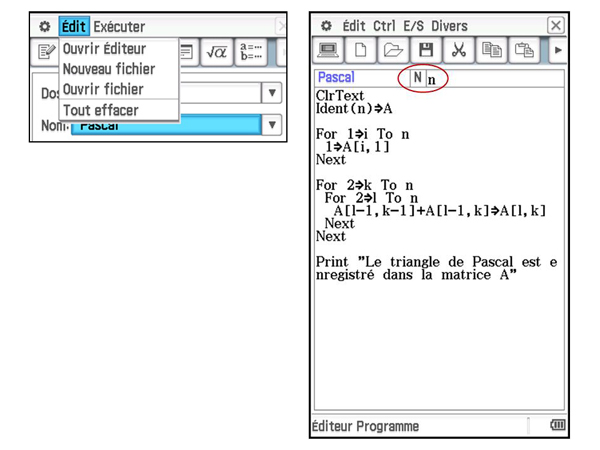
Il est possible de mettre le nombre n directement dans les paramètres du programme (en haut à droite, cerclé de rouge), cela permet d'utiliser ce programme dans le menu Principal. Nous aurons ainsi une visibilité globale sur tous nos calculs : transformées de Fourier et triangle de Pascal.
Voici quelques commentaires et explications :
• Ident(n) génère la matrice identité de taille n ;
• A[l, k] correspond au coefficient de la l ième ligne et de la k ième colonne de A. On utilise le fait que A[l, k] est égal à la somme du coefficient de la ligne du dessus, A[l – 1, k], et du précédent, A[l – 1, k – 1]. On aurait aussi pu concevoir un programme en utilisant les coefficients binomiaux. La touche correspondante,  , se trouve dans le clavier Avancé ;
, se trouve dans le clavier Avancé ;
• Le triangle de Pascal est enregistré dans la matrice A, un message affichera cette information lorsque le programme sera exécuté.
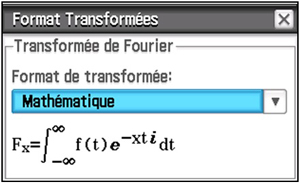
La calculatrice formelle fx-CP400+E propose cinq définitions pour la transformée de Fourier. Nous choisissons ici le format Mathématique dans les paramètres  du menu Principale
du menu Principale  .
.
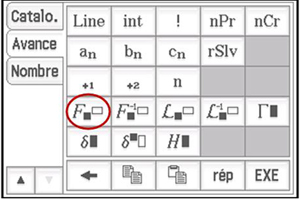
Calculons ensuite la transformée de Fourier de la fonction t ?2n-1 (cost)n, pour plusieurs valeurs de n. La transformée de Fourier se trouve dans le clavier Avancé.
À chaque fois, on affiche les n + 1 premières lignes du triangle de Pascal, la dernière ligne donne les coefficients binomiaux .
Il est plus aisé d'écrire tous les calculs en fonction de n, comme ci-dessous. Il suffit ensuite de changer la valeur de n au début ; la calculatrice refait tous les calculs.
Pour n = 5, on obtient (la fonction désigne la fonction delta de Dirac, définie par
(0) = 1 et
(x) = 0 pour tout réel x non nul) :
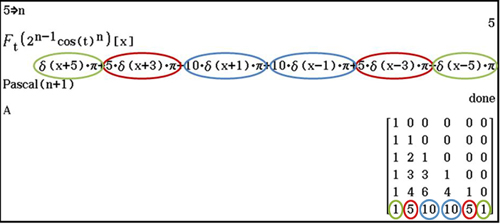
De même, pour n = 8, on obtient :
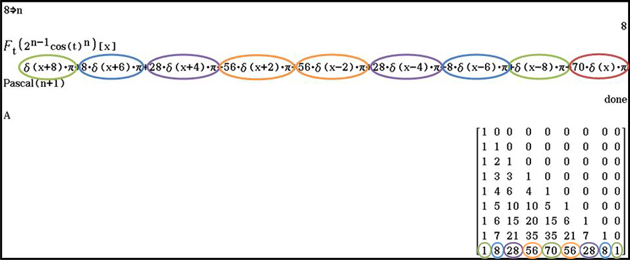
Sans même savoir ce qu'est une transformée de Fourier, on peut établir une conjecture à partir des deux résultats précédents. On trouve en effet :
Vérifions cette relation à l'aide de la calculatrice (Expand est la fonctionnalité de la calculatrice qui permet de développer une expression algébrique, utilisée ici pour distribuer ) :
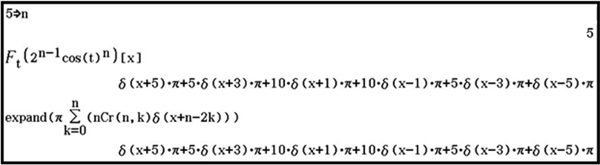
La relation observée est donc bien un résultat mathématique général, comme nous le confirme la calculatrice formelle fx-CP400+E.
