
Pierre Duchet est l’un des rares spécialistes français de combinatoire. Il est un témoin privilégié des grands développements des mathématiques discrètes, des découvertes d’Erdös aux nombres premiers en progression arithmétique, en passant par la démonstration du théorème des quatre couleurs ou de la conjecture de Berge (Claude Berge a été son directeur de thèse).
À quand peut-on faire remonter les débuts de la combinatoire ?
La combinatoire, au sens moderne du terme, est l’étude systématique des structures. On peut la faire remonter aux années 1930. On peut même en situer les origines géographiques : la Hongrie est le pays où la combinatoire est la plus reconnue et développée ! Par exemple, Erdös, Turán, Halmos, Szemerédi, Bollobás, Lovász, Frankl… Tous ces mathématiciens fameux sont nés en Hongrie. Il serait presque plus difficile de citer des spécialistes de combinatoire qui ne seraient pas hongrois ! Aujourd’hui, à part la Hongrie, il existe des écoles de combinatoire nord-américaines, dans l’ex-URSS, dans quelques pays d’Europe de l’Est et, à un degré moindre, en France, et plus récemment au Japon (depuis trente ans) et en Chine (depuis une dizaine d’années).
Cela dit, on pourrait faire remonter la combinatoire au génial Euler, avec son problème des ponts de Königsberg [voir FOCUS]. C’est de la combinatoire structurelle, autrement dit une « manière molle de parler de l’espace ». Ou bien à Laplace et à sa vision atomiste de l’espace et de l’univers. Ou encore à Leibniz, qui, pour « prédire l’avenir », est amené à « découper » des surfaces [allusion au calcul intégral]. Il faudrait aussi parler de Poincaré et de son Analysis situs ! Mais il faut bien l’avouer, la combinatoire ne décolle vraiment qu’avec l’explosion de la recherche opérationnelle (RO) et l’avènement des graphes [voir FOCUS] comme structure mathématique à part entière. Un exemple archétypique, en RO, est le problème du voyageur de commerce : imaginez un représentant en voiture qui doit visiter chacune des N villes d’un pays pour y rencontrer des clients. Son trajet doit minimiser le nombre total de kilomètres parcourus, car l’essence coûte cher. Parmi les N ! trajets possibles, lequel est optimal ? Et quid si toutes les distances valent 1 et que le voyageur doit passer une fois et une seule par chaque ville (problème du circuit hamiltonien) ? Voici le genre de problèmes que pose la recherche opérationnelle. Pour de petites valeurs de N, on connaît la solution, mais très vite on n’a au mieux que des heuristiques pour aider le voyageur de commerce. Ce problème est extrêmement difficile. [Il est dit NP-difficile.] Et l’on revient aujourd’hui aux problèmes posés au XVIIIe siècle. La combinatoire n’est pas apparue par hasard, elle s’inscrit dans un continuum historique.
Problèmes NP-difficiles
Le XVIIIe siècle, Poincaré au début du XXe, les années 1930 et la théorie des graphes, la naissance de la RO durant la Seconde Guerre mondiale… Et que se pase-t-il ensuite ?
 La RO a produit de très nombreux problèmes d’optimisation discrète tels le coloriage de graphes. La recherche d’un algorithme est la finalité de ces problèmes. Une variante importante du problème de coloration d’un graphe est le problème du 5-flot, énoncé par William Thomas Tutte en 1954 [voir FOCUS].
La RO a produit de très nombreux problèmes d’optimisation discrète tels le coloriage de graphes. La recherche d’un algorithme est la finalité de ces problèmes. Une variante importante du problème de coloration d’un graphe est le problème du 5-flot, énoncé par William Thomas Tutte en 1954 [voir FOCUS].
La RO, la théorie des graphes, l’algorithmique, mais également l’étude des systèmes d’ensembles (set systems) appelés aussi hypergraphes (hypergraphs) restent de grands pourvoyeurs de problèmes pour la combinatoire : problèmes de packing (trouver des empilements d’objets aussi denses que possibles dans un espace donné), problèmes de covering (une structure combinatoire en couvre-t-elle une autre ?), conjecture des quatre couleurs (maintenant théorème), conjecture de Hadwiger… La théorie des graphes en était la base, et ces grands problèmes généraient l’activité et toutes les recherches dans le domaine. Mais ce n’est plus vraiment le cas aujourd’hui.
Pourquoi ? Comment les pratiques ont-elles évolué en combinatoire après les années 1970 ?
 Leonhard Euler (1707–1783).
Leonhard Euler (1707–1783).
Aujourd’hui, les grands problèmes ne sont plus les premiers pourvoyeurs des recherches : beaucoup sont largement entamés ou résolus (conjecture de Berge, maintenant théorème fort des graphes parfaits, ou théorème des quatre couleurs).
Dans les années 1970 se développe une théorie de la complexité pour traiter les problèmes de décision (ceux pour lesquels on peut répondre par oui ou par non). On a les problèmes « faciles », de complexité polynomiale. Ils forment ce que l’on appelle la classe P (pour « polynomial »). Pour ces problèmes, on sait trouver, pour les résoudre, un algorithme dont le temps de calcul est majoré par un polynôme de la taille de l’entrée. On a ensuite les problèmes « difficiles, voire carrément impossibles », qui forment la classe dite NP.?Ce sont ceux pour lesquels on connaît une manière « rapide » de vérifier une solution. Enfin, il y a des problèmes pour lesquels on ne sait pas s’ils sont P, NP ou autre chose, et des problèmes qui par nature ne relèvent pas de la théorie de la complexité ! Tous les chercheurs sont persuadés que NP n’est pas incluse dans P. Mais personne n’est capable de le démontrer. Le problème du voyageur de commerce est NP-difficile, c’est-à-dire au moins aussi dur que NP-complet. [Un problème est NP-complet si sa résolution en temps polynomial entraîne la résolution en temps polynomial de tout problème NP.] Un problème NP-difficile est en pratique insoluble. Et l’on s’est aperçu, au cours des années, que beaucoup des grands problèmes qui suscitaient des recherches en combinatoire étaient NP-difficiles. C’est le cas du problème du nombre chromatique total, qui est assez facile à expliquer : on conjecture que le nombre chromatique total d’un graphe G est inférieur à D(G) + 2, où D(G) est le degré maximal des sommets de G. Voyons ce que cela signifie.
Colorer un graphe G avec k couleurs (une k-coloration de G) consiste à attribuer à chaque sommet et à chaque arête de G l’une parmi k couleurs, de telle sorte que deux objets adjacents (arête–sommet, sommet–sommet ou arête–arête) soient toujours de couleurs différentes. Le nombre chromatique total de G est le plus petit entier k pour lequel une k-coloration existe sur G. Déterminer ce nombre est un problème NP-difficile. Mais on peut parfois le caractériser, ou bien le borner.
La conjecture de Hadwiger est un autre problème de coloration non résolu. Supposons que le nombre chromatique du graphe non orienté G soit supérieur à m (ce qui signifie qu’il est impossible de colorer les sommets de G avec moins de m couleurs sans que deux sommets reliés reçoivent la même couleur). Alors G possède m sous-graphes connexes disjoints connectés les uns aux autres par au moins une arête.
Quels sont les outils mathématiques qui ont permis de résoudre, ou au moins d’entamer les problèmes de mathématiques discrètes ?
La boîte à outils du spécialiste en combinatoire comporte un tout petit nombre de résultats fondamentaux. Le premier d’entre eux, sans doute le plus important, est le théorème des mariages. [Soient un ensemble de garçons, un ensemble de filles, et l’application qui associe à chaque garçon les filles qui lui plaisent. Si, pour chaque sous-groupe de garçons, le nombre de filles qui leur plaît est supérieur au nombre de garçons de ce sous-groupe, alors on peut marier chaque garçon à une fille non encore mariée qui lui plaît.] En essayant de généraliser cette problématique, on aboutit à une « théorie des couplages » assez puissante, où la théorie des matroïdes joue un rôle important.

Le mathématicien hongrois Paul Erdös (1913–1996) avec, à sa droite,
Claude Berge (1926–2002).
Sinon, il existe des méthodologies. Par exemple, Paul Seymour et son équipe abordent les problèmes de théorie des graphes avec toujours la même approche de « décomposition » : il s’agit d’arriver à « casser » un graphe donné, de sorte que les seuls graphes « incassables » possèdent une structure connue. Quand on veut assembler un graphe quelconque à partir de briques élémentaires connues, l’art est de trouver la « bonne colle ». Je dois avouer que je ne croyais pas que cette approche permettrait un jour de résoudre la conjecture de Berge, et pourtant…
Pour les problèmes d’optimisation discrète, on essaie souvent de les reformuler de manière linéaire : les contraintes sont modélisées par un système d’inégalités linéaires portant sur les données variables, et le problème revient alors à maximiser (ou à minimiser) une certaine fonction des données, elle-même linéaire. On est alors dans les conditions d’application du théorème fondamental de la programmation linéaire [voir par ailleurs dans ce numéro], avec la différence importante que les optima du problème combinatoire doivent correspondre à des valeurs entières des variables, et non à des valeurs rationnelles (ou réelles) quelconques. Lorsque les structures modélisant le problème sont « sympathiques », on peut prouver que l’optimum en valeurs entières coïncide avec l’optimum fractionnaire.
Sinon, il n’existe que très peu de résultats généraux permettant d’analyser les structures. On fonctionne par analogie. L’équipe de Seymour, toujours elle, a eu l’idée de comparer les graphes à des mots sur une surface. Ainsi, en généralisant un théorème de Kuratowski (qui est polonais !), ils ont élaboré une théorie des mineurs de graphes. En une vingtaine d’articles qui s’étendent sur plus de vingt-cinq ans, ils ont pu démontrer la célèbre conjecture de Wagner [selon laquelle, dans toute famille infinie de graphes, l’un des graphes est isomorphe au mineur d’un autre] !
Quand le Loto inspire un problème non résolu
La « structure » semble fondamentale en combinatoire. Qu’est-ce qu’une « structure » ?
Il faut se méfier du mot « structure » ! Un arbre, un graphe, un hypergraphe, un système d’ensembles… tout cela définit des outils de modélisation qui sont manipulables, qualitativement et quantitativement, par un mathématicien. En revanche, un graphe biparti [un graphe pouvant être colorié en utilisant seulement deux couleurs] fournit bien un outil de modélisation, mais qui n’est pas manipulable. La combinatoire structurelle s’intéresse à tout ce qui est modélisable de manière immédiate comme un ensemble d’ensembles finis ; c’est vaste ! En fait, il faut développer une intuition de ce qu’est une « bonne structure », et pour cela, il faut des outils de représentation. Les diagrammes de Venn, ou « patatoïdes », sont un outil de représentation. De même que la géométrie ou la topologie sont un outil de représentation pour l’espace. D’autres domaines qui étudient les structures sont l’algèbre et la combinatoire algébrique. Mais en algèbre, on définit toujours au minimum une opération sur ladite structure. Nous, on n’a même pas ça ! On s’intéresse à la connectivité entre les éléments (savoir s’ils sont reliés, connectés).
Quelles sont les grandes théories qui ont été élaborées pour étudier les structures ?
La théorie des graphes pose de très nombreux problèmes intéressants, plus qu’elle n’en résout. Et encore : quand on passe des graphes non orientés aux graphes orientés, on effectue un saut de complexité phénoménal ! C’est la jungle ! Nous avons aussi parlé de la combinatoire structurelle. Il faut mentionner également la combinatoire énumérative, liée au dénombrement (compter avec une méthodologie donnée). Le dénombrement concerne l’aspect quantitatif des structures (sont-elle nombreuses, rares ? Combien y en a-t-il exactement, asymptotiquement ?). Les problèmes de dénombrement sont abondants. Faire de la combinatoire sur les nombres, par exemple, revient à révéler des structures arithmétiques particulières.
Un autre domaine important est la théorie de Ramsey, selon laquelle on a toujours de l’ordre dans une structure, pourvu qu’elle soit « suffisamment grande ». Une question typique de cette théorie est : « Quel est le nombre minimum d’éléments à réunir pour que je sois sûr que telle propriété soit vérifiée ? » En fait, cette théorie provient de problèmes extrémaux très généraux. Un exemple simple est le problème du Loto : combien de grilles différentes devez-vous cocher au minimum pour être certain d’avoir (mettons) quatre numéros gagnants ? Ce problème, malgré bien des recherches, est toujours non résolu ! Un problème extrémal, au sens général, consiste à minimiser une fonction à trois paramètres k, n et t. L’entier n est la taille de l’ensemble de référence (n = 49 nombres dans le cas du Loto), k est le nombre d’éléments des parties considérées (on coche toujours k = 6 numéros pour une grille de Loto). Enfin, t est le nombre minimal d’éléments des parties que l’on s’impose de couvrir (pour le Loto, on demande que t = 4 bons numéros soient garantis). C’est ça, un problème extrémal : minimiser le cardinal de la famille T des parties à k éléments telle que, quelle que soit la partie E à t éléments, on soit assuré de trouver un ensemble F, dans la famille T, qui contienne E. En dehors de quelques cas triviaux, on ne sait pas résoudre ces problèmes.
Pour enchaîner avec les grands domaines de la combinatoire, il faut parler de la théorie des configurations (design theory). C’est une théorie des structures régulières.?En voici un exemple : dans un dodécaèdre, il s’agit de la disposition de tous les cubes formés par huit des sommets du dodécaèdre. Les polyèdres réguliers, les codes correcteurs d’erreur, les réseaux sont des configurations.
L’un des grands problèmes dans cette théorie est la classification des plans projectifs [voir FOCUS]. C’est un très vieux problème. Plus généralement, on se pose la question de l’existence de t-configurations. Récemment, on a réussi à montrer qu’il n’existe pas de plan projectif d’ordre 10. Mais au-delà de 10, et au-delà des plans projectifs, on ne sait pas beaucoup de choses…
La théorie des nœuds et des tresses relève également de la combinatoire : le diagramme d’un nœud est la combinatoire d’une courbe ! Comment reconnaître si un nœud est trivial ? Comment dénouer un nœud dont on sait qu’il est trivial ? Ces questions sont d’une difficulté redoutable.
On fait de la combinatoire sans le savoir
À vous entendre, la combinatoire semble omniprésente ! Quelle est sa place au sein des mathématiques ?
Beaucoup de mathématiciens font de la combinatoire sans le savoir. Mais en fait, en 2010, les mathématiques discrètes ne sont toujours pas reconnues en tant que domaine autonome. Absentes des grands congrès internationaux, elles sont encore vues comme un outil, et non comme un objet d’études. Voire comme des considérations d’informaticiens ! C’est très injuste : si les problèmes semblent a priori plus faciles dans le monde continu que dans le monde discret (où ils sont souvent inattaquables), c’est peut-être parce que le continu est une approximation de la réalité. Je vois les réels comme une commodité de modélisation qui cache la forêt de la réalité. Le discret possède de nombreuses applications en chimie moléculaire et en physique atomique ! Il existe une authentique vision combinatoire du monde. Il n’en reste pas moins difficile d’attirer les étudiants vers la combinatoire.
La raison ? Les maths discrètes ne font pas l’objet d’une théorie bien hiérarchisée. On n’y trouve pas vraiment de profondeur théorique, les problèmes sont difficilement reliables [sic.] les uns aux autres. Mais c’est un défaut de jeunesse, cette théorie ne demande qu’à acquérir de la maturité. Mon collègue américain Jack Edmonds, lui, sait poser des bons problèmes en optimisation. [Dans la même pièce, Edmonds est en train de déchiffrer Tangente 131, consacré aux mathématiques aux États-Unis.] Un « bon problème », c’est un problème qui est dans NP et dans co-NP.
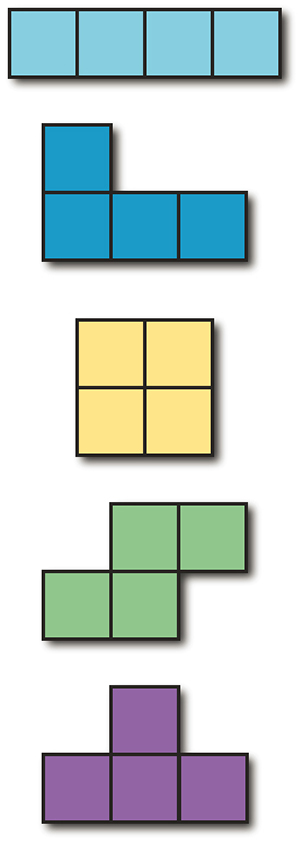
Les cinq polyminos d’ordre 4 (ou tétraminos).
Quelles sont donc les grandes problématiques générales abordées par les spécialistes de combinatoire aujourd’hui ?
Eh bien, tout théorème min-max est considéré comme important, car révélateur de l’existence d’une structure. Ainsi, une généralisation de la problématique des mariages est de chercher le nombre maximal d’ensembles disjoints dans une famille d’ensembles donnés.?C’est ça, le problème de paquement (ou packing problem). Le problème d’optimisation dual consiste à couvrir tous les éléments avec le minimum d’ensembles possibles : c’est le problème de couverture (ou covering problem). Les graphes parfaits sont un exemple de théorème min–max : le nombre minimal de couleurs nécessaires pour colorer un graphe parfait (son nombre chromatique) coïncide avec le nombre maximal de sommets deux à deux reliés (sa plus grande clique). Cette propriété caractérise les graphes parfaits.
Sinon, pour changer complètement de registre et parler d’objets plus simples, on a tous les problèmes concernant les polyminos, ces objets géométriques élémentaires constitués de petits carrés unitaires collés les uns aux autres. Quand on assemble deux carrés, on obtient… un domino. Eh bien, on ne sait pas dénombrer le nombre de polyminos constitués de n carrés, pas même de façon asymptotique (on conjecture qu’il y en a moins d’une constante multipliée par 4n).
Autre problème symptomatique de l’enfer que ces petites bêtes nous font voir : considérons un polymino quelconque. On cherche à le paver avec des barres horizontales de taille 3 (des triminos horizontaux) et des dominos verticaux, de telle sorte que tout le polymino soit couvert, et que ni les triminos ni les dominos ne se chevauchent. Savoir si vous pouvez paver ainsi votre polymino est un problème NP-complet ! C’est consternant… Cela dit, je conjecture que si l’on se restreint aux polyminos simplement connexes (c’est-à-dire sans trous), alors le problème redevient traitable…
 Endre Szemeredi (né en 1940).
Endre Szemeredi (né en 1940).
Enfin, la théorie des nombres fourmille de problèmes ouverts, en particulier grâce à Erdös (conjectures d’Erdös–Szemeredi et d’Erdös–Turan, problème de discrépance d’Erdös, qui fait l’objet d’intenses recherches actuellement..). Mais là, les mathématiciens ont frappé fort : Ben Green et Terence Tao ont montré en 2005 qu’il existe des progressions arithmétiques de longueur arbitraire dans l’ensemble des nombres premiers. Ils utilisent des outils de combinatoire additive, et une théorie nouvelle que l’on appelle maintenant théorie ergodique. Comme quoi, les succès existent parfois !
