Il existe au moins deux façons d'associer un triangle équilatéral à un triangle T quelconque, autrement dit de « sortir » un triangle possédant le maximum de symétries d'un triangle qui n'en possède a priori aucune au départ.

La première consiste à construire le triangle formé par les sommets de l’hypocycloïde de Steiner (voir En Bref "L'enveloppe des droites de Simson d'un triangle"). La seconde fait intervenir le triangle de Morley, qui est formé par les trisectrices des trois angles au sommet.
Il y a un rapport entre les deux constructions : les côtés des deux triangles équilatéraux sont deux à deux parallèles (mais les deux triangles sont orientés en sens inverse).
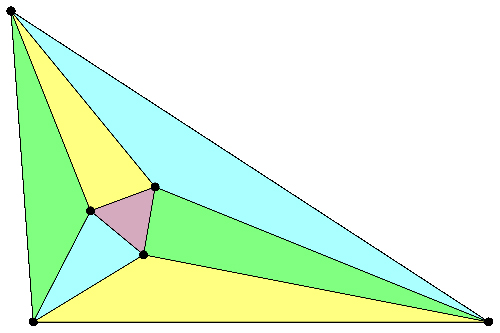
Le petit triangle construit à partir des trisectrices d’un triangle quelconque initial est équilatéral.
