
La géométrie du triangle est inépuisable. Parmi les innombrables richesses que l’on peut y dénicher, deux résultats à l’aspect similaire sortent du lot : les théorèmes de Ceva et de Ménélaüs. Commençons déjà par nous munir d’un triangle ABC. Plaçons un point P sur (BC), un point Q sur (CA) et un point R sur (AB). Enfin, il sera commode d’utiliser la notion de mesure algébrique des longueurs : tout segment UV pourra être affecté d’un signe. La mesure algébrique du segment [UV] sera égale à sa longueur si l’on va de U vers V, et à l’opposé de sa longueur si l’on va de V vers U. C’est tout ce dont on a besoin pour énoncer les théorèmes de Ménélaüs et de Ceva !
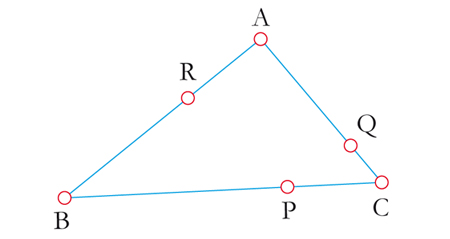
La configuration de base des théorèmes de Ménélaüs et de Ceva.
T
héorème de Ménélaüs :
les points P, Q et R sont alignés si, et seulement si,
Théorème de Ceva :
les droites (AP), (BQ) et (CR) sont concourantes ou parallèles si, et seulement si,
