
Le birapport, l’un des piliers de la géométrie projective, qui s’exprime aussi bien en termes réels avec la division harmonique qu’en termes complexes, permet à la fois des constructions aisées et des démonstrations élégantes. Non seulement il aide à la résolution de problèmes géométriques qui, sans cela, pourraient s’avérer délicats, mais il permet l’accès à des raisonnements épurés.
La division harmonique pour éviter des calculs
La version « soft » de ce fameux birapport est la division harmonique. On retrouve dans cet adjectif le mot grec « armonia » et sa connotation musicale chez Pythagore. En effet, si une corde fixée à ses deux extrémités D et B (D donnant le do) est pincée en son milieu A, on obtient par vibration le do une octave au-dessus. Si maintenant on la pince en C, au tiers de [AB], on obtient le sol : c’est cela, armonia. On dira à la Renaissance que DC est moyenne harmonique entre DB et DA, ce que l’on traduit par l’égalité ou encore, avec les notations de la figure,
soit
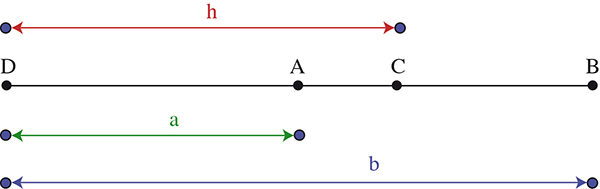
L’harmonie d’une corde vibrante.
De musicale, la notion est devenue géométrique au XVIIe siècle ; on dira que les points A, B, C, D sont en division harmonique, vocabulaire que l’on trouve déjà chez le mathématicien et musicien Philippe de La Hire (1640–1718).
Avec la notation « mesure algébrique » (voir FOCUS), deux siècles plus tard, on dira que les quatre points alignés (A, B, C, D), que l’on a l’habitude d’utiliser avec les points C et D étant l’un intérieur, l’autre extérieur au segment [AB], forment une division harmonique, ou encore que C et D sont conjugués harmoniques par rapport à A et B. Cela équivaut à écrire
Cette notion de géométrie affine a fait les beaux jours de générations d’élèves de lycée, qui l’ont rencontrée dans nombre de leurs problèmes et qui, traduite algébriquement, a donné lieu à bien des formules, mais c’est plus l’aspect géométrique d’introduction à la géométrie projective que celui purement calculatoire que l’on retiendra dans l’usage de la division harmonique.
Que se passe-t-il en effet si le point C est milieu de [AB] ? On ne peut plus alors trouver de point D « visible » tel que la relation précédente soit vérifiée : on dit alors que D est le point à l’infini de la droite (AB). Ce passage à la limite prend consistance dans le petit problème suivant. Dans un trapèze ABCD, où les côtés parallèles sont [AB] et [CD], les droites (AD) et (BC) se coupent en I, les droites (BD) et (AC) se rencontrent en J. K est milieu de [AB] et L de [CD]. On peut de multiples façons – par calcul vectoriel ou analytique, par calcul barycentrique, avec des homothéties ou des symétries obliques… – démontrer que les point I, J, K et L sont alignés, mais l’essentiel n’est pas là. L’important ici est que (I, J, K, L) soit une division harmonique, puisque tous deux égaux (grâce au théorème de Thalès) à
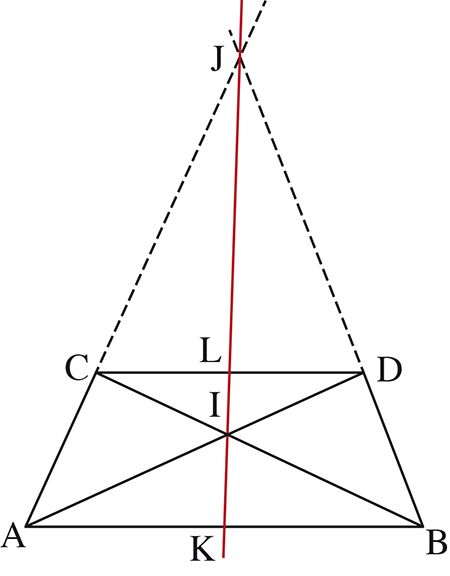
Que se passe-t-il si le trapèze devient un rectangle, avec (AC) parallèle à (BD) ? On est dans le cas limite évoqué précédemment : I devient milieu de [KL] et J est le point à l’infini dans la direction de (AC) et (BD).
Les faisceaux de droites
Plus féconde encore que celle de division harmonique est la notion de faisceau harmonique de droites (voir l'article « Un invariant par projection centrale »). Il s’agit cette fois d’un ensemble de quatre droites concourantes ou parallèles passant chacune par les points d’une division harmonique. On démontre par des considérations d’homothéties que les intersections (A, B, C, D) de ces quatre droites avec toute sécante sont elles-mêmes en division harmonique et – propriété intéressante – que, dans le cas de droites sécantes en O, la parallèle à (OA) menée par B coupe les droites (OC) et (OD) en deux points dont B est le milieu. C’est cette propriété que l’on utilise pour construire un faisceau harmonique. C’est aussi cette particularité qui permet de montrer que deux droites sécantes et les bissectrices des angles qu’elles forment constituent un faisceau harmonique.
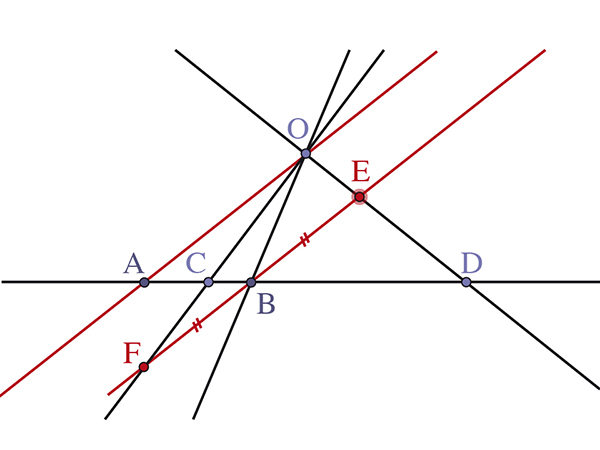
Allons plus loin : l’existence même de ce faisceau harmonique permet de démontrer que les pieds des bissectrices [AD) (intérieure) et [AE) (extérieure) issues du sommet A du triangle ABC divisent le côté opposé à A en segments proportionnels aux côtés [AB] et [AC]. Performant, le faisceau harmonique, non ?

[AD) et [AE) bissectrices équivaut à DB / DC = EB / EC = AB / AC.
Si (BG) est parallèle à (AE), en jumelant les faits que le faisceau des quatre droites (AE), (AB), (AD), (AC) est harmonique,
que le triangle ABG est isocèle et le théorème de Thalès, on prouve cette condition nécessaire et suffisante.
La généralisation au birapport
On a vu apparaître, avec la division harmonique, deux quotients, dont on peut encore faire le quotient : ce sera le birapport, déjà utilisé discrètement par les géomètres de l’Antiquité comme Pappus ou Apollonius, et que le mathématicien français Michel Chasles (1793–1880) nommait rapport anharmonique. Ainsi, étant donnés quatre points alignés A, B, C et D, le birapport de (A, B) et (C, D) est-il égal à . Dans le cas de (A, B, C, D) en division harmonique, il est égal à – 1.
Cette notion de birapport, à la base de la géométrie projective, revêt de multiples aspects.
Le birapport de quatre nombres, réels ou complexes, noté (a, b, c, d) ou parfois [a, b, c, d], désigne la quantité
Le birapport Δ de quatre droites concourantes ou parallèles se définit ainsi : si ces droites coupent une sécante en A, B, C et D, alors Δ est le birapport des quatre points d’intersection, dont on démontre qu’il est indépendant de la sécante choisie (voir démonstration dans l'encadré « La formule de Möbius »).
Un point O étant choisi, le birapport de quatre points A, B, C et D d’un même cercle est celui des quatre droites (OA), (OB), (OC), (OD).
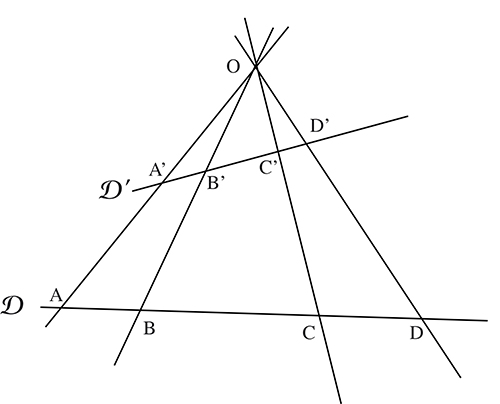
Parmi les multiples propriétés du birapport, l’une est fondamentale : quatre points du plan complexe sont cocycliques ou alignés si leur birapport est un nombre réel. Que de jolies applications de cette propriété la géométrie n’a-t-elle pas fournies ! Elle peut en effet être d’une aide très efficace dans la démonstration de certains résultats.
Un bel exemple est celui de l’un des énoncés de l’Olympiade russe de géométrie en honneur d’Igor Sharygin (1937–2004) donné en 2019 :
Les quadrilatères ABCD et A1B1C1D1 sont symétriques par rapport à un point P. On sait de plus que A1BCD, AB1CD et ABC1D sont inscriptibles (c’est-à-dire que leurs sommets sont cocycliques, ou appartiennent à un même cercle). Démontrer que ABCD1 l’est aussi.
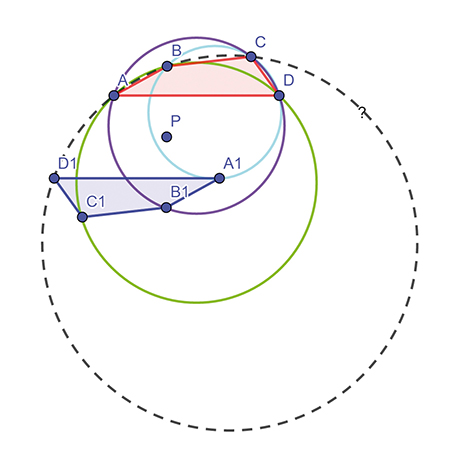
On peut bien sûr, pour y arriver, faire une énorme « chasse aux angles »… mais il faut savoir débusquer les « bons » angles inscrits ! On peut aussi, et très rapidement, utiliser le birapport, et alors quelques calculs suffisent…
Choisissons astucieusement P comme origine (affixe 0) et appelons a, b, c, d les affixes respectives de A, B, C, D. Celles de A1, B1, C1, D1 seront alors, dans l’ordre : – a, – b, – c, – d. Traduisons maintenant les cocyclicités successives :
• de A1, B, C, D : le birapport est réel ;
• de A, B1, C, D : le birapport est réel également ;
• de A, B, C1, D : le birapport est encore réel.
On en déduit que le produit de p et q, divisé par r, est toujours réel. Or :
et donc
soit encore
Cette relation traduit exactement la cocyclicité de A, B, C, D1 ! Efficace, non ?
