
En 1933 à Budapest, quelques étudiants en mathématiques, dont Paul Erdős et George Szekeres, avaient l’habitude de se réunir. Esther Klein proposa un jour le problème suivant : soient cinq points du plan en position générale, montrer que quatre d’entre eux peuvent former un quadrilatère convexe, c’est-à-dire un polygone dont les diagonales ne passent pas par son extérieur.
Ce joli résultat se démontre avec un peu de réflexion et une analyse au cas par cas. Erdős le surnomma happy ending problem car il déboucha notamment sur le mariage de George Szekeres et Esther Klein (voir Tangente 172, 2016) !
Le problème connut un prolongement plus mathématique. Pourquoi ne s’intéresser qu’aux quadrilatères ? On peut en effet se demander combien de points il faut placer dans le plan en position générale pour être certain d’y trouver un polygone convexe à n côtés. Le cas n = 5 a été résolu en 1935 : il faut un ensemble de neuf points pour être sûr d’y trouver un pentagone convexe.

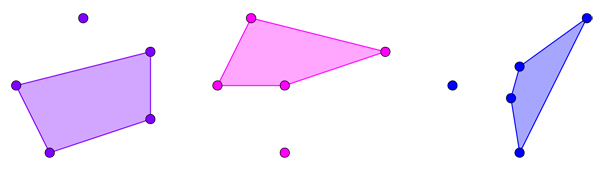
Dans cette configuration, on ne peut former aucun pentagone convexe.
Erdős et Szekeres ont prouvé dès 1935 que ce minimum existe pour tout entier n et qu’il est inférieur à
Ils ont démontré vingt-cinq ans plus tard que ce minimum est supérieur à 2n-2 +1.
En 2005, Szekeres et son étudiante Lindsay Peters ont démontré qu’il faut un ensemble de dix-sept points pour être certain d’y trouver un hexagone convexe. Aucun autre résultat n’est connu actuellement.
