
Antoine Rolland (troisième en partant de la gauche) reçoit son Trophée, réalisé par Denise Demaret-Pranville, en présence de Gilles Cohen, Frédéric Jaëck et Bertrand Hauchecorne. Il est maître de conférence en statistique à l’Université Lyon-II.
Au pays du Démocristan, le Parlement est composé de quatre-vingt-dix-neuf députés. Une loi, pour être votée, doit recueillir la majorité des suffrages et donc être approuvée par cinquante députés au minimum. Il se trouve que seuls trois partis siègent : le parti A a quarante-neuf sièges, le parti B en a quarante-neuf aussi, et le parti C, un seul. Supposons que les députés soient disciplinés et votent tous de la même manière au sein de chaque parti. Ni A, ni B, ni C n’a la majorité absolue à lui seul, mais toute coalition de deux partis est gagnante. Dans cette configuration, les trois partis sont interchangeables et ont donc le même pouvoir… avec des nombres de sièges très différents !
À qui perd gagne
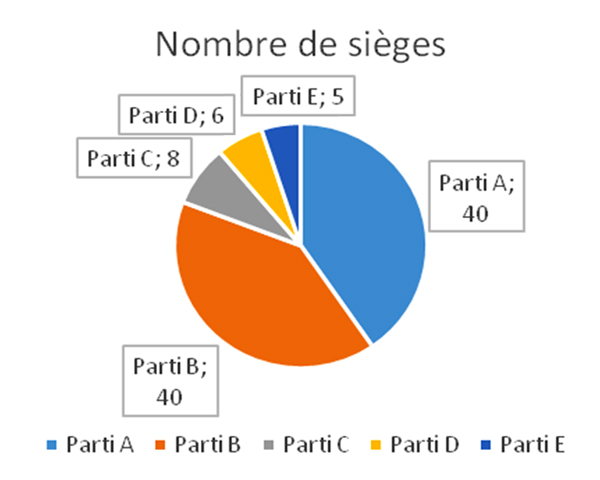
De nouvelles élections ont lieu, et deux partis supplémentaires se présentent devant les électeurs. Les résultats donnent quarante sièges au parti A, quarante à B, huit à C, six à D et cinq à E. La coalition {A, B} est toujours gagnante, mais {A, C} et {B, C} ne le sont plus. Une alliance avec le seul parti C n’est plus suffisante aux deux « grands » partis A et B pour former une coalition gagnante : la présence de D ou E est devenue nécessaire ; C est donc moins puissant qu’auparavant. Ainsi, les partis A et B, qui ont perdu des sièges, ont gardé le même pouvoir, mais le parti C, qui a gagné des sièges, en a perdu !
L’exemple (simplifié) du Démocristan montre qu’on ne peut se limiter au nombre de députés dans un parti pour déterminer son pouvoir. Pour approcher au mieux cette notion de pouvoir, plusieurs « indices » ont été développés en théorie des jeux.
Pour définir des « indices de pouvoir » généraux, on considère une situation où n individus, dotés respectivement des poids w1, w2… wn , participent à un processus de vote à la majorité simple. Une coalition est alors un ensemble d’individus, et cette coalition est gagnante si la somme des poids des individus la composant dépasse la moitié de la somme totale des poids. Dans le cadre du Parlement, les individus sont des partis, et les poids correspondent au nombre de députés de chaque parti.

John Banzhaf (né en 1940).
Un indice de pouvoir très élémentaire est proposé en 1965 par John Banzhaf, un juriste américain attaché à la notion d’équité et de justice. Il utilise la notion d’« individu décisif ». Au sein d’une coalition gagnante, un individu est décisif si la coalition n’est plus gagnante sans lui. L’indice de Banzhaf d’un individu consiste à compter le nombre de coalitions gagnantes dans lesquelles cet individu est décisif. Son indice de Banzhaf normalisé est obtenu en divisant son indice de Banzhaf par la somme des indices de Banzhaf de tous les individus, de telle sorte que la somme des indices normalisés de tous les individus vaut 1.
Dans le cadre initial du Démocristan, le parti A est décisif dans les deux coalitions {A, B} et {A, C} ; son indice de Banzhaf normalisé est donc égal à 1/3, tout comme ceux de B et de C : les trois partis ont le même indice de pouvoir. Après les élections, l’indice de pouvoir de A (comme celui de B d’ailleurs) est égal à 2 / 7, et ceux de C, D et E sont égaux à 1/ 7 : le pouvoir de A et B a donc un peu baissé. Celui de C a, lui, beaucoup baissé, même s’il a plus de députés qu’auparavant.
D’autres indices de pouvoir sont possibles. En 1954, Lloyd Shapley et Martin Shubik, alors à l’université de Princeton (États-Unis, New Jersey), en avaient déjà proposé un permettant de calculer le pouvoir d’un individu au sein d’une coalition. On considère toutes les permutations des candidats. Si par exemple ils sont 3, A, B et C, elles sont au nombre de 6 : ce sont ABC, ACB, BAC, BCA, CAB, CBA. D’une manière générale, il y en a n! = 1 2 … n. Pour chacune d’elles, on additionne successivement, et dans l’ordre, les poids des individus de la permutation, jusqu’à dépasser strictement la moitié de la somme des poids (c’est-à-dire que les premiers termes de la permutation correspondent à une coalition gagnante). L’individu qui a permis d’atteindre ce résultat est l’élément décisif de la permutation. L’indice de Shapley–Shubik d’un individu est le nombre de permutations où il est décisif, divisé par le nombre total de permutations, c’est-à-dire n!. Ceci permet de normaliser l’indice de telle sorte que la somme de tous les indices de Shapley–Shubik soit égale à 1.
Revenons au Démocristan : avec seulement trois partis, la situation est symétrique et chacun est décisif dans deux permutations sur les six possibles : les indices de Shapley–Shubik de A, B et C sont donc identiques et égaux à 1/3. Après les élections, il faut regarder les cent vingt permutations possibles des cinq groupes parlementaires : A est décisif dans trente-six cas, B pareillement, et C, D et E sont décisifs dans seize cas chacun. Les indices de Shapley–Shubik valent donc 9/30 pour A et B et 4/30 pour C, D et E.
Les propriétés mathématiques du pouvoir
Dans un article paru en 2003 (la Mesure du pouvoir de vote, Mathématiques et Sciences humaines 163), Nicolas-Gabriel Andjiga, Frédéric Chantreuil et Dominique Lepelley recensent près d’une dizaine d’indices de pouvoir différents et montrent qu’ils peuvent tous se formaliser d’une manière générique, en comptant le nombre de coalitions où un individu est décisif, et en affectant toutes ces coalitions d’un poids spécifique (voir en encadré).
Des indices génériques
Si N est l’ensemble de tous les individus, la forme générale d’un indice de pouvoir P (i) de l’individu i est
La somme porte sur les coalitions S, de poids w(S), au sein de N, dont i est membre ; δ est la fonction indicatrice, valant 1 si S est une coalition gagnante et 0 sinon ; S\{ i } est la coalition S privée de i.
L’indice de Banzhaf B(i ) correspond au cas = 1 ;
l’indice de Banzhaf normalisé B’(i ) est obtenu par
L’indice de Shapley–Shubik SS(i ) correspond au cas
et donc
Une étude des indices de pouvoir permet de déterminer quelques propriétés techniques. Si un individu a possède un poids plus important que b, alors son pouvoir ne peut pas être inférieur à celui de b (propriété de monotonie). Si a donne une partie de son poids à b, alors le pouvoir de a ne peut pas augmenter (propriété de transfert). Si a et b forment un bloc, c’est-à-dire se comportent comme un individu de poids total égal à la somme des poids de a et b, alors le pouvoir de ce bloc doit être au moins aussi important que la somme des indices de pouvoir de a et b (propriété de bloc).
Les indices de Banzhaf et de Shapley–Shubik vérifient ces trois propriétés. Étonnamment, l’indice de Banzhaf normalisé ne vérifie que la monotonie.
Le respect de ces propriétés permet d’éviter les situations paradoxales : la non-satisfaction de l’une d’elles correspond à une situation où plus de poids pour un individu lui donne moins de pouvoir ! Autrement dit, il vaudrait mieux parfois ne pas gagner les élections… En fait, en théorie des jeux, le pouvoir réel d’un individu n’est pas exactement égal à son poids ; il n’est donc pas étonnant que, parfois, certaines situations de pouvoir apparaissent comme mathématiquement paradoxales.

Martin Joseph Shubik (1926–2018) était spécialisé dans l’analyse stratégique.
Au Parlement européen
Abandonnons le Démocristan et regardons le pouvoir des différents groupes au sein du Parlement européen élu en mai 2019, à un moment où la situation de l’appartenance de la Grande-Bretagne à l’Union européenne était assez floue. On dénombre sept groupes constitués : Groupe du Parti populaire européen (PPE) ; Alliance progressiste des socialistes et démocrates (S&D) ; Alliance des démocrates et des libéraux pour l’Europe (ADLE), maintenant renommée Renew Europe ; Groupe des Verts/Alliance libre européenne (Verts/ALE) ; Groupe Europe des Nations et des libertés (ENL) ; Conservateurs et réformistes européens (CRE) ; Gauche unitaire européenne/Gauche verte nordique (GUE/NGL). Au sein des non-inscrits peuvent encore se constituer deux groupes cohérents : le Parti du Brexit et le Mouvement 5 étoiles. Il y a donc au total dix groupes différents, en considérant abusivement que les députés non-inscrits votent de manière identique.
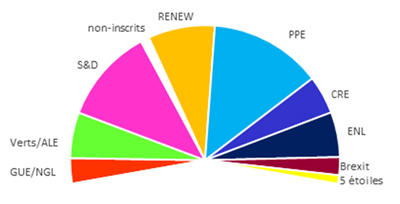
Le Parlement européen après les élections de 2019.
Le calcul de l’indice de Banzhaf normalisé de chacun des groupes parlementaires se calcule en parcourant les 210 = 1 024 sous-ensembles possibles et en regardant pour chacun les groupes décisifs. Le calcul de l’indice de Shapley–Shubik se calcule en parcourant les 10! = 3 628 800 permutations différentes et en notant, pour chacune, quel est le groupe décisif.
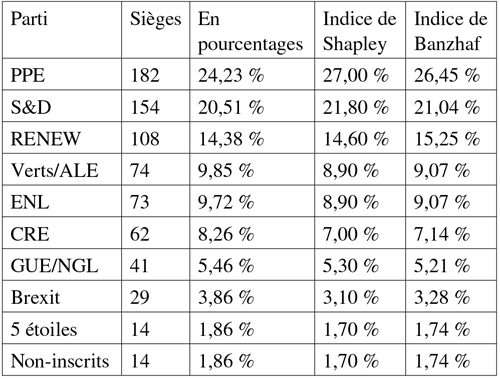
Répartition des sièges par parti au Parlement européen,
et indices de Shapley–Shubik et Banzhaf normalisés.
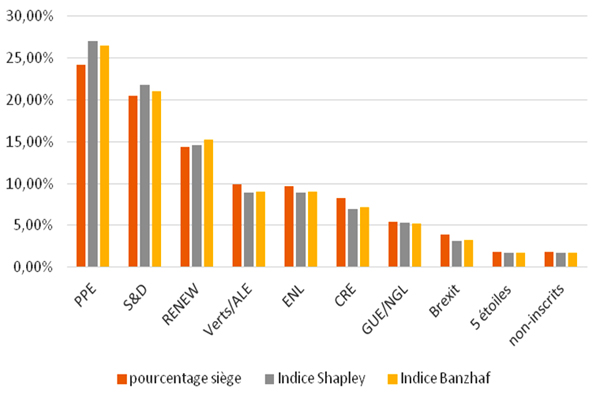
Ce graphe permet de comparer les indices de pouvoir
aux pourcentages de sièges détenus par chaque parti.
L’analyse de ces résultats (voir le tableau) montre que les « grands » partis PPE et S&D ont un pouvoir au sein du Parlement plus important que ce que leurs nombres respectifs de sièges laissait penser. A contrario, les « petits » partis tels que les Verts ou l’ENL ont un pouvoir moindre que leur poids au Parlement. Les deux indices, sans être strictement identiques, ne sont « pas très éloignés » l’un de l’autre, et traduisent une même réalité : dans un contexte d’émiettement des partis, le pouvoir des « grands » se trouve renforcé (par rapport aux « petits ») car ils sont plus nécessaires à la formation de coalitions gagnantes. Comme quoi, il ne suffit pas de maîtriser l’art de la campagne électorale pour remporter les élections : il faut aussi être à l’aise avec la théorie des jeux…
Cet article a reçu le Prix Tangente du meilleur article 2019.
