
Les coordonnées polaires sont une autre façon de représenter les points d’un plan euclidien muni d’un repère orthonormé (voir encadré dans article « Des équations pour les courbes »). On passe aisément du couple ( ρ, θ ) de coordonnées polaires d’un point M à celui de ses coordonnées cartésiennes via les relations x = ρ cos θ et y = ρ sin θ.
Ce qui est intéressant, c’est qu’une courbe du plan peut alors être définie par une équation polaire, relation entre ρ et θ. Un cercle de centre O et de rayon R ou une droite passant par O faisant un angle α avec ont une équation simple (respectivement ρ = R ou θ = α ). Mais dans le cas général une droite ou un cercle sont représentés par des équations plus sophistiquées.
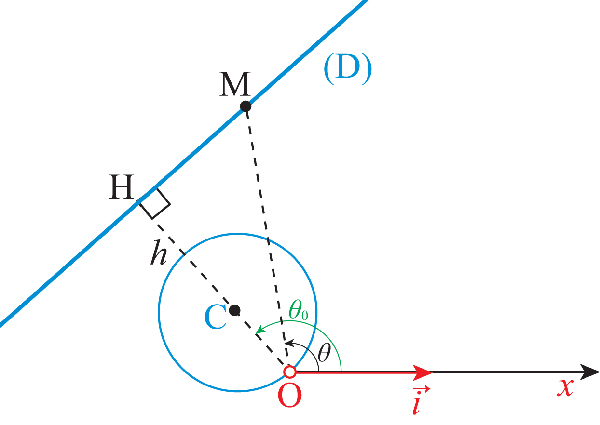
Ainsi, ρ = h / cos (θ – θ0 ) est l’équation polaire de la droite faisant avec l’angle θ0 + π/2 et située à une distance h de l’origine (voir figure). On peut en déduire l’équation polaire d’un cercle passant par l’origine en remarquant que le transformé par inversion* de pôle O d’une droite ne passant pas par O est un cercle passant par O.
Ainsi, un cercle de rayon R passant par O dont le centre C est sur la droite (OH) aura pour équation polaire ρ = 2R cos (θ – θ0 ).
* Une inversion de pôle P et de puissance k transforme un point M en un point M’ situé sur la droite (PM) tel que le produit des mesures algébriques et
soit égal à k.
Cercles et rosaces

Pièces phares des cathédrales, éléments hautement décoratifs utilisés en architecture, les rosaces sont au départ des courbes évoquant la forme d’une rose avec ses pétales, inscrites dans un cercle et à tracer à la règle et au compas. Les premiers plans de la grande rosace de la cathédrale de Strasbourg (Bas-Rhin), par exemple, sont l’œuvre d’Erwin de Steinbach en 1320. Prouesse technique de l’art gothique elle se trace à partir du partage d’un cercle en trente-deux « pétales » puis d’ogives et de cercles concentriques créés à partir de ce partage.
Il existe des rosaces plus « savantes », définies par leur équation polaire ρ = a cos (nθ ), en quelque sorte des sinusoïdes en coordonnées polaires, qui ont été étudiées par le mathématicien italien Guido Grandi entre 1723 et 1728. Elles ont, pour n impair, n pétales et, pour n pair, 2n pétales.
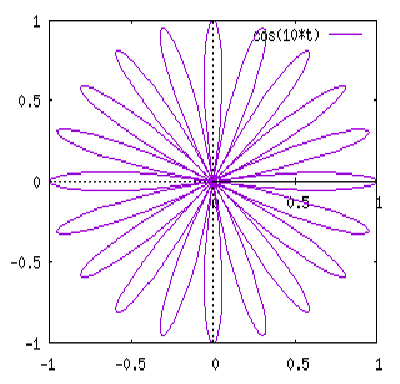
Rosace à vingt pétales d’équation polaire ρ = cos(10 θ ).
Les spirales
Autre courbe harmonieuse, la spirale a été elle aussi abondamment utilisée en architecture, tant pour décorer des chapiteaux de colonnes que des portails de fer forgé.
Les formes les plus courantes de spirales rencontrées en art sont celles que l’on peut tracer au compas seul, à plusieurs centres, faites de cercles raccordés tangentiellement, et la spirale d’Archimède, d’équation polaire ρ = a θ.

Spirales décoratives à la maison carrée de Nîmes (Gard).

Motif en spirale de fer forgé.
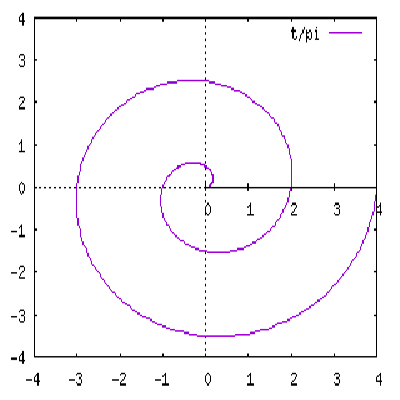
Spirale d’Archimède d’équation polaire ρ = θ /π.
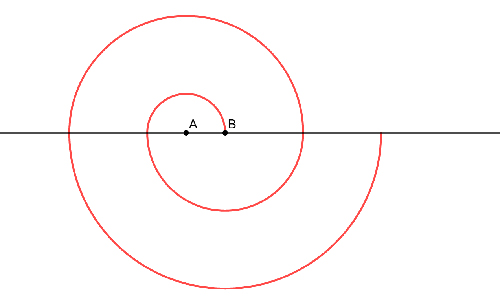
Spirale à deux centres A et B.
