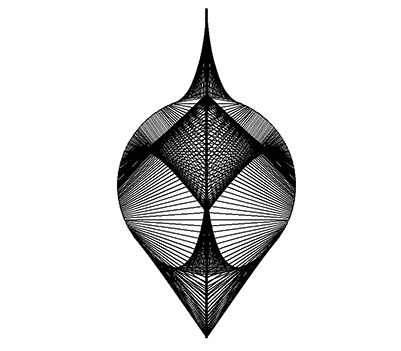
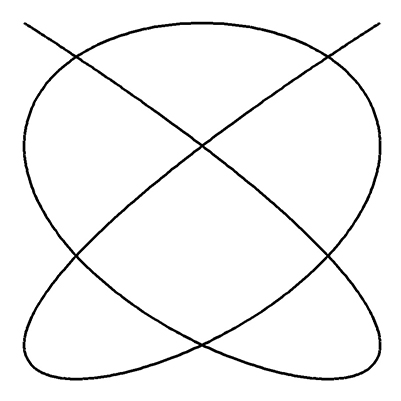
Les courbes de Lissajous
Les courbes de Lissajousm (a, b, φ) peuvent être définies par les équations paramétriques x (θ) = Ra sin(a θ), y (θ) = Rb sin(b θ + φ), avec a et b deux entiers naturels (les paramètres ou fréquences). Pour nos applications, a et b seront deux entiers relatifs. R a et R b sont deux réels positifs, l’angle θ varie entre 0 et 2π, et φ (le déphasage) varie entre 0 et π/(2a). Elles ont notamment été étudiées par le physicien français Jules Lissajous (1822 −1880).
Fixons a un entier naturel non nul. Les courbes de Lissajous m (a, a, π /2) décrivent des cercles, les courbes m (a, 2a, π/2) sont des portions de paraboles, tandis que les m (2a, a, π/2) représentent des « 8 » caractéristiques.
Dans la terminologie de l’auteur, certaines courbes, appelées tresses, ont deux axes de symétrie. D’autres, les cornes, montrent deux points de rebroussement et soit un axe, soit un centre de symétrie. La corne la plus simple est l’arc de parabole ; le cercle et le « 8 » sont les plus simples des tresses. Pour φ = 0, si a + b est impair, on a une tresse, si a + b est pair, c’est une corne. Si φ augmente de π/(2a), à une tresse succèdera une corne, et réciproquement.
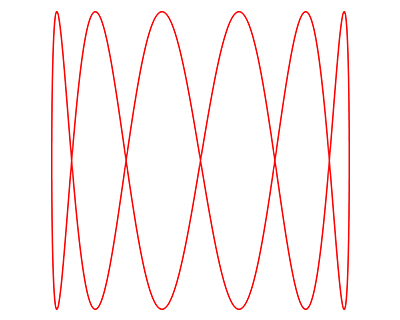
Courbe de Lissajous avec Ra =Rb =1, a = 1, b =6 et φ = 0.
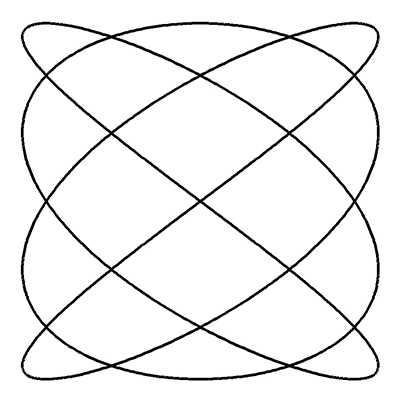
Les tresses possèdent deux axes de symétrie.
Les cornes possèdent un axe ou un centre de symétrie.
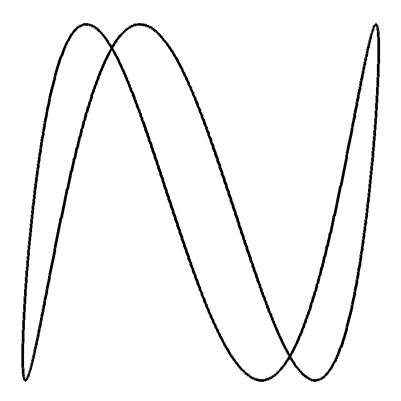
Une courbe de Lissajous qui n’est ni tressée, ni cornue.
Monovirettes et bivirettes
Pour l’auteur, une monovirette est une courbe de Lissajous m (a, b, φ). Une bivirette, ou virette à deux couches, est la somme de deux courbes de Lissajous ; son expression paramétrique est donc :
x (θ) = R a1 sin(a1θ) + R a2 sin(a2θ), y (θ) = R b1 sin(b1θ + φ1) + R b2 sin(b2θ + φ2)
avec a1, a2, a3, a4 quatre entiers relatifs.
On prendra pour simplifier R a1 = R a2 = R b1 = R b2 = 1 et φ1 = φ2= π/2.
L’étude de ces bivirettes « simplifiées » donne déjà lieu à d’intéressantes questions de combinatoire (combien d’axes ou de centres de symétrie, en fonction des fréquences ?), et à de merveilleuses courbes graphiques.
De manière générale, une k-virette ou virette à k couches est la somme de k courbes de Lissajous. Plus k augmente, plus les motifs obtenus sont variés, mais plus leur étude est rendue difficile.

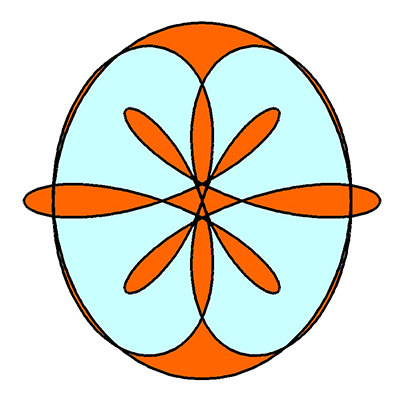
Les bivirettes m ( 2, 2, π /2 ) + m ( 5, 7, π /2 ) et m ( 7, 7, π /2 ) + m ( 3, 5, π /2 ).
Les striades
Une striade, ou virette à striures (expressions proposées par l’auteur), est une k-virette avec k ≥ 2 telle que les courbes de Lissajous dont elle est issue sont, graphiquement, reliées par des striures (entre la première courbe et la somme des deux courbes, pour des valeurs de θ équiréparties entre 0 et 2π ). Visuellement, ces courbes suggèrent parfois un « effet de relief » qui peut intéresser les artistes et les graphistes.