Les identités remarquables
Qu'ont-elles de si remarquable, ces fameuses « identités » ? Pourquoi certaines héritent-elles de ce qualificatif ? Ce ne sont pourtant pas les formules élégantes et concises qui manquent en mathématiques... Mais ne boudons pas notre plaisir, et revenons sur ces relations.
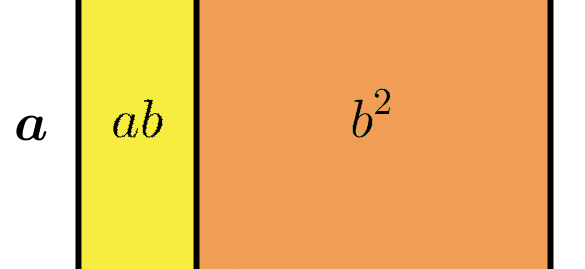
LES ARTICLES
Des identités aux applications remarquables
Fabien Aoustin
Les identités remarquables étudiées au collège (et maintenant en début de lycée…) peuvent s'avérer bien utiles pour trouver les solutions de certaines équations, dont celles du second degré. Le tout est de savoir où se cachent ces mystérieuses identités !
Identités remarquables en classe
Élisabeth Busser
« Trouver deux nombres connaissant leur somme et leur produit. » Ce problème, déjà posé par les Babyloniens il y a quatre mille ans, a fait date dans l'histoire des mathématiques, ouvrant la voie à toute une culture d'enseignement : celle des identités remarquables.
En bref : Qu'est-ce qu'une identité remarquable ?
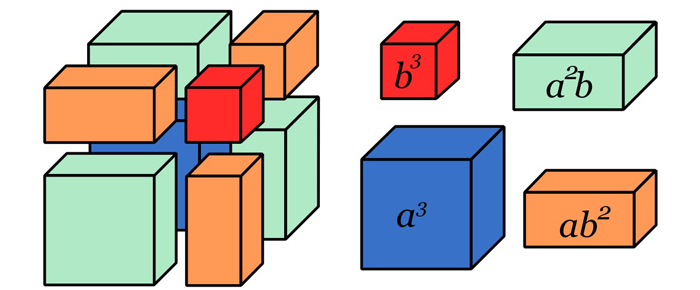
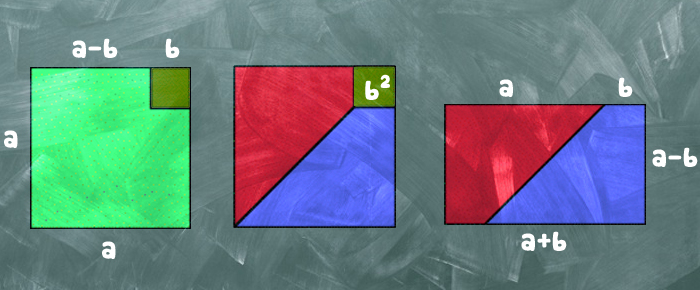
Fabien Aoustin et Hervé LehningLes identités remarquables sont un grand classique du lycée. Petits rappels en images...
En bref : Identités remarquables en séries
Gilles CohenQue ce passe-t-il si l'on essaye de calculer des sommes comprenant un nombre de terme de plus en plus élevé ? C'est l'enjeu de l'étude des suites et des séries.
En bref : La formule de Newton
Hervé LehningQuelle postérité ! La formule du binôme de Newton trouve des applications aussi bien en trigonométrie qu'en probabilités…
Les dernières publications POLE
