Calculs d'aires
On l'appelait à l'origine « surface », du même nom que ce qu'elle mesurait… L'aire des figures planes se devait d'être calculée depuis longtemps pour des raisons ancrées dans le réel ! Partager un champ de manière équitable, soumettre un domaine à l'impôt le plus juste possible nécessitent un calcul précis et incontestable. Durant l'Antiquité, les Égyptiens et les Grecs procédaient par approximations successives, une méthode longue et fastidieuse, surtout quand intervient ce nombre insaisissable que nous appelons aujourd'hui π.
Il faudra plusieurs siècles pour que les scientifiques fondent le calcul intégral, qui résout en pratique tous les cas que l'on peut rencontrer, de l'aire du champ de maïs à celle balayée par une planètes durant sa révolution autour du soleil.
Il faudra plusieurs siècles pour que les scientifiques fondent le calcul intégral, qui résout en pratique tous les cas que l'on peut rencontrer, de l'aire du champ de maïs à celle balayée par une planètes durant sa révolution autour du soleil.

LES ARTICLES
À peu près π
Benoît Rittaud
On peut jouer avec les aires pour calculer π, mais on peut aussi partir de π pour choisir des aires. Pour changer, plutôt que la célèbre méthode d'exhaustion d'Archimède, on peut remettre au goût du jour une approche historique sans doute due aux Égyptiens... Ferez-vous mieux ?
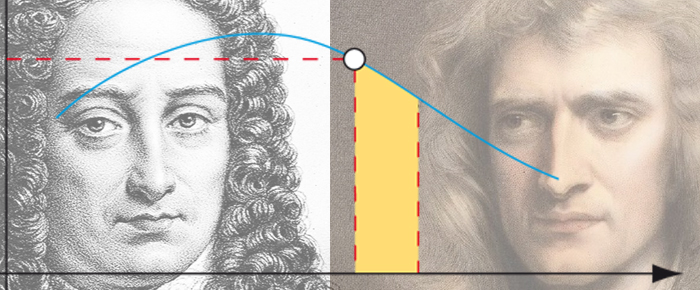
Aires et primitives, une liaison intime
Hervé Lehning
Aires et primitives sont associées depuis les travaux fondateurs de Leibniz et de Newton au XVIIe siècle. Ce lien a permis de simplifier le calcul de nombreuses surfaces du plan, mais la relation entre aire et intégrale est en fait bien plus profonde que cette question calculatoire.
L'intérêt des coordonnées polaires
Daniel Justens
L'usage du calcul intégral pour les calculs d'aires est parfois peu commode en coordonnées cartésiennes. Le passage aux coordonnées polaires peut alors être d'une aide appréciable. Il permet aussi le calibrage de la distribution normale en probabilité.
La loi des aires de Kepler
Benoît Rittaud
Elle porte le numéro 2 dans la liste des lois de Kepler, mais c'est pourtant elle que l'on démontre le plus facilement. La loi des aires est l'un des trois résultats de l'astronome allemand qui, à l'aube du XVIIe siècle, a révolutionné notre vision du monde céleste.
En bref : Brèves de l'aire
F. Aoustin, É. Busser et H. LehningDécouvrez différentes méthodes de calcul d'aire de polygones