1001 - L'as du pic
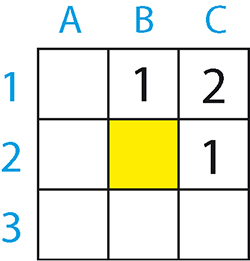Un alpiniste possède des grilles dont les cases contiennent des entiers strictement positifs figurant l'altitude des zones d'un massif montagneux. Dans ces grilles, chaque nombre autre que 1 est la somme d'un nombre situé sur la même ligne et d'un nombre situé sur la même colonne que lui. Le plus grand nombre de la grille est le « pic ». 1A. Complétez la grille de l'alpiniste ci-contre de taille 3 × 3 (un nombre et un seul par case) de sorte que la case jaune (2B) contienne le pic le plus grand possible.
2A. Quelle est le plus grand pic possible d'une grille 4 × 4 de l'alpiniste ?
1002 - Le cerf-volant perdu de vue
Le cerf-volant du Père Dudevue vient de disparaître dans les nuages. Son propriétaire cherche à le reconstituer. Il se rappelle simplement que c'est un quadrilatère dont les diagonales sont deux segments sécants mesurant respectivement 105 et 116 centimètres.
1A. À partir de cette seule information, quelle serait, en cm2, la plus grande aire possible du cerf-volant ? À la réflexion, le Père Dudevue se rappelle qu'il connaît aussi le périmètre de son cerf-volant : 290 cm.
2A. Quelle est alors, en cm2, la plus grande aire possible du cerf-volant ? (arrondir si besoin les réponses au nombre entier le plus proche)
1003 - Tours de carte
Devant la carte de ce restaurant gastronomique (tous les prix sont des nombres entiers d'euros), Alice, qui souhaite commander deux plats, hésite. Elle calcule ce que coûterait chacune des six combinaisons de deux plats parmi les quatre qu'elle préfère, et décide de choisir entre les quatre combinaisons les moins chères, dont les prix sont : 59 €, 65 €, 66 € et 69 €.
1A à 1D. Quels sont, dans l'ordre croissant, les prix des 4 plats ?
Bob, quant à lui, hésite entre cinq plats, pas forcément les mêmes qu'Alice. Il calcule les montants des dix combinaisons de deux plats parmi ceux qu'il préfère. Les cinq montants les plus bas sont : 56 €, 64 €, 66 €, 69 € et 70 €.
2A à 2D. Quels sont, dans l'ordre croissant, les prix des 4 plats les moins chers ?
1004 - Chemin unique
Un damier de trois cases sur une est dessiné avec des traits de contour noirs.
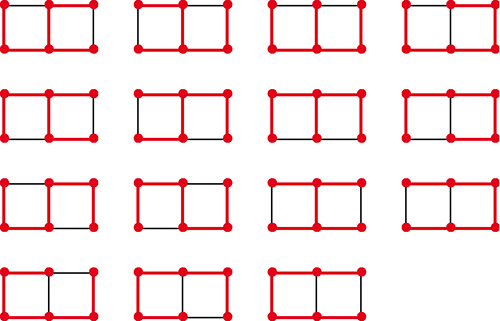
Vous désirez surligner en rouge certaines arêtes de manière à permettre de relier, d'une façon et d'une seule, n'importe quel sommet des carrés qui le composent à n'importe quel autre en suivant un tracé rouge.
1A. De combien de façons différentes peut-on tracer les traits rouges ? (le dessin ci-après montre les 15 façons de colorier un damier de deux cases sur une).
2A. Même question avec un damier de six cases sur une.
3A. Même question avec un damier de deux cases sur deux.
1005 - Ruben's Cube 
Ruben veut découper à la scie un grand cube de bois en 64 petits dés de même taille. La scie fait ses coupes suivant un plan, et Ruben peut changer la disposition des morceaux après chaque coupe.
1A. Combien de coupes lui faudra-t-il, au minimum, pour obtenir les 64 dés ?
Après la découpe, Ruben peint chaque face de chaque dé en bleu, en jaune, en rouge ou en noir. Il le fait de façon à pouvoir, en assemblant tous les dés, reconstituer, selon son désir, un grand cube bleu, ou un jaune, ou un rouge, ou un noir.
2A. Sachant que 40 dés exactement possèdent les quatre couleurs sur leurs faces, combien Ruben a-t-il peint de dés bicolores ?
1006 - Qui peut le + peut le –
Sur le dernier relevé bancaire d'Alice, figure en haut de page le solde de fin du mois dernier. Puis, sur les lignes qui suivent, 12 nombres entiers non nuls (1 par ligne) correspondent aux opérations du mois. Le nombre est positif s'il s'agit d'un crédit sur le compte, négatif s'il s'agit d'une dépense.
Curieusement, chaque nombre des lignes 1 à 10 est strictement supérieur au total des deux lignes qui suivent.
De plus, les lignes 11 et 12 sont identiques aux lignes 1 et 2.
1A. Combien y a-t-il, au plus, de nombres positifs sur les lignes 1 à 10 ?
2A. Sachant que le compte est à 10 € en fin de mois et que le maximum de lignes positives a été atteint, quel était le solde minimum de fin du mois dernier ?
1007 - Ines Presso : « Math else ? »
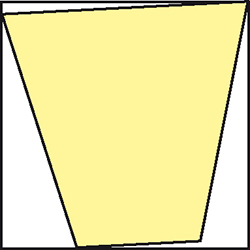Vous pouvez découvrir ci-contre la projection d'une capsule de café et de son étui. La capsule se projette selon un trapèze de petite base 16 mm, les trois autres côtés ayant chacun 32 mm de longueur. Le trapèze est inscrit dans un carré : la projection de l'étui. Ines Presso, conceptrice de l'emballage, a réussi à économiser du carton en diminuant le côté du carré selon le modèle ci-contre : carré et trapèze ont un sommet confondu, deux autres sommets du trapèze touchant des côtés du carré.
1A. Quelle est, en mm, la longueur d'une diagonale du trapèze ?
2A. Quelle est, en mm2, l'aire du carré ? (arrondir les réponses à deux décimales sans écrire d'unité)
1008 - Une ribambelle de dossards
Après une compétition d'athlétisme, Larry Bambel, l'entraîneur, range les dossards des cadets, numérotés entre 1 et 2341, dans plusieurs caisses, de sorte qu'un numéro et son triple ne soient jamais dans la même caisse.
1A. Quel est le plus grand nombre possible de dossards dans une même caisse ?
Les dossards des minimes, numérotés de 1 à 2N, sont répartis entre deux piles A et B (de N chacune). Larry prend le plus grand numéro de la A, le plus petit de la B, enregistre leur écart (en valeur absolue) et range les deux dossards dans un carton ; il recommence avec les dossards restants et additionne l'écart au précédent, et ainsi de suite jusqu'à l'épuisement des piles. En suivant un processus analogue, Larry range ensuite les dossards des benjamins, moins nombreux que les minimes, numérotés de 1 à 2P. Le total des écarts des deux catégories est 2341.
2A et 2B. Quel est le nombre 2N de minimes (2A) et quel est le nombre 2P de benjamins (2B) ? (s'il y a plusieurs solutions, indiquer celle qui maximise la case 2A)
1009 - Trop bons, les trombones !
Un papetier possède des chaînes de trombones attachés à la suite les uns des autres. Lors d'une « manipulation », il détache un trombone à ses deux extrémités et obtient ce trombone ainsi que deux nouvelles chaînes plus petites.
1A. À partir d'une chaîne de 63 trombones, combien de manipulations devra-t-il effectuer au minimum pour être capable de fournir, sans nouvelle manipulation, n'importe quel nombre de trombones entre 1 et 63 ?
1B. Quelle est la plus longue chaîne initiale qui permet, en 8 manipulations, de fournir n'importe quel nombre de trombones compris entre 1 et la longueur de la chaîne ?
Le papetier reçoit une chaîne formée de 200 trombones de trois couleurs différentes : le premier est rouge, le deuxième bleu, le troisième vert. Il remarque qu'en enlevant un trombone sur quatre (à partir du quatrième), la suite des 50 trombones enlevés est identique à la suite des 50 premiers trombones de la chaîne initiale et la suite des 150 restants est identique à celle des 150 premiers trombones de la chaîne initiale.
2A, 2B, 2C. Quel est le nombre de trombones rouges (2A), bleus (2B) et verts (2C) de la chaîne ?
1010 - Moyennant quoi…
Alice écrit les nombres entiers de 1 à 19 sur un tableau (une fois chacun). Elle en choisit deux de même parité, et les remplace par leur moyenne. Elle recommence 18 fois jusqu'à n'obtenir qu'un seul nombre.
1A, 1B, 1C,1D, 1E, 1F. Quels sont les nombres qu'elle ne pourra jamais obtenir à l'arrivée ? (commencer à la 1A).
Bob écrit les nombres entiers de 1 à 19 sur un tableau. Il en choisit quatre dont la somme est un multiple de 4, et les remplace par leur moyenne. Il recommence 6 fois jusqu'à n'obtenir qu'un seul nombre.
2A, 2B, 2C,2D, 2E, 2F. Quels sont tous les nombres qu'il pourra obtenir à l'arrivée ? (on les écrira par ordre croissant ; attention, toutes les cases ne sont pas forcément à remplir)
1011 - Hep, taxi !
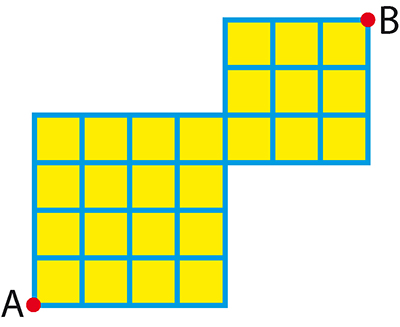
Autour des 25 blocs immobiliers carrés de Cubic-City, les côtés, mesurant tous 1 km, sont des routes à double sens. Un autobus part de A pour aller en B. Il peut passer 2 fois par le même carrefour, mais jamais 2 fois par la même route.
1A. Quelle est le nombre de km du plus long chemin qu'il puisse parcourir entre A et B ?
Deux taxis partent au même moment, l'un de A vers B, l'autre de B vers A. Ils roulent sans arrêt à la vitesse constante de 26 km/h, suivant chacun l'un des chemins les plus courts (13 km). Quand un taxi a le choix entre deux directions, il choisit l'une des deux avec la probabilité 1/2.
2A, 2B. Quelle est la probabilité qu'ils se croisent (à mi-chemin) ? (le résultat est à donner sous forme de fraction irréductible : son numérateur en 2A et son dénominateur en 2B).
1012 - Le triangle maudit
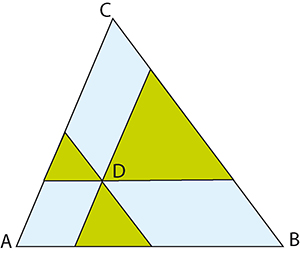Le triangle ABC, dangereux pour la navigation, a pour aire 756 km2 et pour côtés des nombres entiers de km (AB mesure 42 km). Pour chaque point D où un navire a sombré, une association a tracé une carte où les parallèles aux côtés de ABC passant par D délimitent trois « triangles de recueillement ». Pour le naufrage du Père Dition, le périmètre de chacun de ces triangles est égal à la longueur du côté de ABC avec lequel il possède un côté commun.
1A. Quelle est, en mètres, la distance du point de naufrage du Père Dition au côté AB ?
Pour le naufrage de la Cool Douce, la somme des aires des triangles de recueillement est la plus petite possible.
2A. Quelle est, en mètres, la distance entre les deux lieux de sinistre ? Les réponses attendues aux deux questions sont des nombres entiers. Arrondir, si nécessaire, à l'entier le plus proche.
1013 - Sans étoile, le monde ne suffit pas
La calculatrice de l'agent 007 possède une « étoile », la touche *, qui effectue une opération secrète. Cette opération possède les propriétés suivantes pour tous les entiers naturels a et b : 0 * (a + 1) = (0 * a) + 1 et (a + 1) * (b + 1) = (a * b) + 1.
Parfois, le résultat coïncide avec la multiplication. Ainsi,
271 * 287 = 271 × 287 (= 77 777) et 2 018 * 39 = 2 018 × 39.
1A. Quel est le plus petit entier d supérieur à 287 tel qu'il existe un entier c inférieur à d vérifiant c * d = c × d ?
2A. Quel est l'entier naturel e supérieur à 2 017 tel que 2 017 * e = 2 017 × 40 ?
3A, 3B. Quels sont les entiers naturels f tels que f * 2 017 = 40 × 2 017 ?
1014 - Le nombre pile… de piles
Dans un tiroir, il y a un nombre pair de piles électriques du type « AA ». On sait qu'il y en a autant de bonnes que de mauvaises. Pour les tester, Alice ne dispose que d'une lampe torche, qui s'allume à condition que les deux piles qu'on y insère soient bonnes. Elle annonce à Bob qu'il lui faudra au maximum 6 essais pour faire marcher la lampe.
1A, 1B, 1C, 1D, 1E. Combien y a-t-il de piles « AA » dans le tiroir ? S'il y a plusieurs solutions, les écrire dans l'ordre croissant sur la ligne 1, du plus petit au plus grand nombre.
Quelques semaines plus tard, Bob se trouve confronté à la même situation, alors qu'il y a 20 piles dans le tiroir (10 bonnes et 10 mauvaises).
2A. Au bout de combien d'essais Bob est-il sûr de pouvoir allumer la lampe ?
1015 - Les deux font la paire
Lors de la superfinale 2016 de ce concours de jeux mathématiques, il y avait autant de questions que de finalistes.
Chaque question a été résolue par tous les concurrents sauf trois. Les organisateurs ont remarqué que si on prenait deux concurrents au hasard, ils n'avaient jamais, à eux deux, résolu l'ensemble des questions.
1A. Combien y avait-il, au plus, de finalistes en 2016 ?
Lors de la finale 2017, le nombre de concurrents avait augmenté. Il y avait toujours autant de questions que de finalistes et, cette fois, chaque question avait été résolue par tous les concurrents sauf quatre. Avant même d'établir le classement, les organisateurs ont calculé que dans ces conditions il y aurait forcément deux finalistes qui, à eux deux, auraient résolu l'ensemble des questions.
2A. Combien y avait-il, au moins, de finalistes en 2017 ?
1016 - Des carrés en somme
Alice écrit les entiers de 1 à 8. Elle les sépare en deux groupes de quatre et s'aperçoit que la somme des carrés des nombres du premier groupe (celui qui contient 1) est égale à la somme des carrés des nombres du deuxième groupe.
1A, 1B, 1C. Quels sont, dans l'ordre croissant, les trois autres nombres du premier groupe ?
Alice recommence alors l'expérience avec les nombres de 21 à 28.
2A. De combien de façons peut-elle les séparer en deux groupes de quatre tels que la somme des carrés du premier groupe soit égale à la somme des carrés du deuxième groupe ?
Bob tente la même expérience avec les nombres de 1 à 12.
2B. De combien de façons peut-il les séparer en deux groupes de 6 tels que la somme des carrés du premier groupe soit égale à la somme des carrés du deuxième groupe ?
2C. Et en deux groupes inégaux ?
1017 - Le pizzaiolo se met en quatre
(Tous les résultats seront arrondis à l'entier le plus proche.)
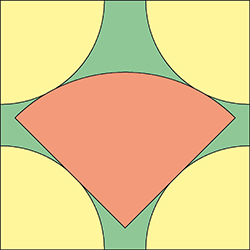Le pizzaiolo donne deux coups de couteaux perpendiculaires passant par un même point situé à 5 cm du centre d'une pizza ronde de 20 cm de diamètre. Il donne à Bob deux parts opposées par le sommet (dont celle qui contient le centre), à Alice les deux autres. Il a choisi l'orientation de la coupe pour que Bob ait la portion la plus grande possible.
1A. Combien Bob aura-t-il de cm2 de pizza de plus qu'Alice ?
Le lendemain, il donne encore à chacun deux parts opposées par le même sommet que la veille. Cette fois, ses quatre coups de couteau découpent sur le bord de la pizza quatre arcs de même longueur.
2A. Combien Bob peut-il avoir, au maximum, de cm2 de pizza de plus qu'Alice ?
Le troisième jour, il apporte, sur un plateau carré, quatre quarts de la même pizza, calés aux coins, et offre un quart d'une pizza de 30 cm de diamètre, tangent aux quatre morceaux (voir dessin).
3A. Quelle est, en cm2, l'aire du plateau ?
1018 - Dites « quatre-vingt-dix-neuf »
François, mathématicien fasciné par les grands nombres, en a trouvé un doté d'une propriété tout à fait étonnante : si on écrit un « 1 » à la gauche et un « 1 » à la droite de cet entier naturel de moins de 100 chiffres, alors on obtient un nombre 99 fois plus grand que lui.
1A, 1B, 1C. Quels sont les 9 derniers chiffres du nombre de François ? (dans le même ordre que ceux du nombre de François, le chiffre des unités à droite).
2A, 2B, 2C. Quel est son nombre de chiffres ?
1019 - Volte-face
Alice et Bob, assis du même côté de la table, jouent à « volte-face ». 6 cartes, numérotées de gauche à droite de 1 à 6, ont une face bleue et une face rouge (la couleur visible des cartes au départ est aléatoire). Chacun des deux joueurs, à son tour, choisit une « carte meneuse » parmi celles numérotées 1 à 4 dont la face visible est bleue, puis retourne la carte meneuse et les deux suivantes. Celui qui ne peut plus jouer a perdu. Le gagnant marque 20 points moins le nombre total de coups joués durant la partie, le perdant marque ce nombre de coups. Chacun joue pour le mieux. Alice commence.
1A. Si toutes les cartes sont face bleue au départ, qui gagnera ? Alice ou Bob ?
1B. Quel est alors le nombre total de coups joués si chacun cherche à optimiser son score ?
1C. Parmi les 16 orientations possibles des cartes de 1 à 4 au départ, combien permettent à Alice de gagner ?
Le lendemain, même jeu, mais cette fois avec des cartes numérotées de 1 à 12, celles de 1 à 10 pouvant être meneuses.
2A, 2B, 2C. Toutes les cartes sont face bleue au départ. Combien de cartes seront meneuses un nombre impair de fois ?
1020 - La sincérité si je mens
Autour de la table 1, sont assis seize habitants de la planète Logique, dont la population est exclusivement composée de Sincères (les S, qui disent toujours la vérité) et de Menteurs (les M, qui mentent toujours).
Les seize convives de la table 1 disent la même phrase : « Mes deux voisins immédiats sont des M ».
1A, 1B, 1C. Combien y a-t-il de menteurs autour de la table 1 ?
Les douze convives de la table 2 disent eux aussi une même phrase : « Mes deux voisins immédiats sont un M et un S ».
2A, 2B, 2C. Combien y a-t-il de menteurs autour de la table 2 ?
Autour de la table 3, il n'y a que huit convives. Quatre d'entre eux disent « Mes deux voisins immédiats sont des M » tandis que les quatre autres disent : « Mes deux voisins immédiats sont un M et un S ».
3A, 3B, 3C. Combien y a-t-il de menteurs autour de la table 3 ?
1021 - Démocratie avancée
Dans ce pays très en avance sur la démocratie, les élections municipales permettent d'élire dans chaque commune les conseillers de manière très particulière. La taille du conseil municipal, fixée par décret, dépend de celle de la commune.
Les candidatures sont individuelles. Une fois le nombre de candidats validé, il est décidé pour combien d'entre eux chaque électeur a l'obligation de voter (ni vote blanc, ni nul ne sont autorisés). Après le vote, une synthèse est faite par un programme informatique qui détermine le conseil municipal avec une condition qui ne souffre aucune exception : chaque électeur y trouvera au moins l'un des candidats pour lesquels il a voté. Lors des dernières élections, dans la petite ville où habite Alice, afin d'élire 10 conseillers, chaque électeur devait voter pour 10 des 25 candidats.
1A. Quel était, au plus, le nombre de votants de la ville d'Alice ?
Dans la ville moyenne où habite Bob, il y avait 55 555 électeurs et 33 candidats. Par coïncidence, comme chez Alice, le nombre de candidats pour lesquels chaque électeur devait voter était égal à la taille du conseil municipal.
2A. Quel était, au minimum, ce nombre ?
1022 - Puzzle en T
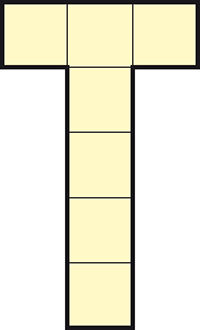Le but de ce puzzle est de ranger sans chevauchement sur un « grand carré » quatre pièces identiques en forme de T.
Chaque pièce est composée de deux branches rectangulaires, l'une faite de trois petits carrés juxtaposés ayant chacun 50 mm de côté, l'autre d'un nombre N de petits carrés de la même taille dont une extrémité rejoint à angle droit le milieu de la première branche. On appelle la pièce un NT ; le dessin représente un 4T.
1A. Quel est, au minimum, la taille d'un côté du grand carré si on peut y placer quatre 1T ?
2A. Et si on peut y placer quatre 2T ?
3A. Et quatre 3T ?
Finalement, l'auteur du puzzle, qui a la folie des grandeurs, choisit le nombre N suffisamment grand pour que le plus petit des « grands carrés » pouvant contenir quatre NT en contienne un cinquième.
4A. Quel est alors la taille d'un côté de ce grand carré minimal ?
Toutes les réponses seront données en mm et arrondies si besoin à l'entier le plus proche.
1023 - Multiplications mystérieuses
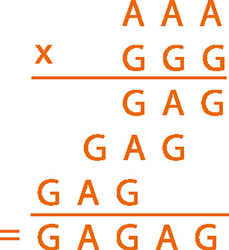
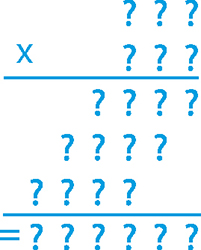
Dans la première multiplication (en bleu), tous les chiffres, représentés par des « ? » sont premiers (ils ne peuvent être que 2, 3, 5 ou 7).
1A, 1B, 1C. Écrivez son résultat.
Dans la deuxième multiplication (en orange), les « A » représentent des chiffres impairs (1, 3, 5, 7 ou 9), les « G » des chiffres pairs (0, 2, 4, 6 ou 8).
2A, 2B, 2C. Écrivez son résultat.
Pour chaque question, s'il n'y a qu'une réponse, la mettre dans la case A. S'il y en a plusieurs, les écrire dans l'ordre croissant à partir de la gauche, en s'arrêtant à la colonne C, même s'il y a plus de trois réponses possibles.
1024 - Cibles mouvantes
Sur un quadrillage de 5 carrés sur 5, une cible rouge est placée au hasard sur un des 25 carrés, dont le fond est du même rouge. Dans un premier temps, la cible est donc invisible. Après chaque tir, la cible se déplace vers une case adjacente du quadrillage, de manière aléatoire.
Le tireur est un expert, qui ne manque jamais la case visée, et cherche à atteindre la cible en un minimum de tirs.
Quand il tire sur une case, cette dernière devient blanche. Si la cible revient dessus, il la verra et ne la manquera pas.
1A. Au bout de combien de tirs, au maximum, est-il sûr d'atteindre la cible ?
Sur un quadrillage de 9 carrés sur 1, une autre cible est placée. Après chaque tir, elle se déplace encore vers une case adjacente de manière aléatoire. Cette fois, la case ne change pas de couleur et la cible reste invisible, sauf si elle est atteinte.
2A. Au bout de combien de tirs, au maximum, le tireur est-il sûr d'atteindre la cible ?
1025 - En l'honneur de 1025
Vingt-cinq mathématiciens assistent à la représentation du Mage Hic. Le point d'orgue du spectacle est le moment où le mage doit deviner des nombres entiers, compris entre 0 et 1025, que les mathématiciens ont choisis entre eux avant le début du spectacle. Pour trouver chacun de ces nombres, le mage doit poser des questions, une au plus par mathématicien, auxquelles les seules réponses autorisées sont « oui » ou « non ».
1A. Quel nombre minimum de questions le mage doit-il poser pour être certain de trouver le premier nombre, sachant que les mathématiciens interrogés doivent dire la vérité ?
Pour le deuxième nombre, il est convenu qu'un des mathématiciens mentira s'il est interrogé, les autres disant la vérité. Mais le mage ne sait pas lequel, ni s'il fait partie des mathématiciens interrogés !
2A. Quel nombre minimum de questions le mage doit-il poser pour être certain de trouver le deuxième nombre ?
1026 - Compte tours
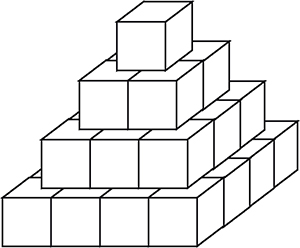
Un promoteur construit une tour pyramidale formée de trente cubes, tous de même taille, disposés comme ci-contre : seize au premier étage, neuf au deuxième, quatre au troisième et un au quatrième. Chaque cube porte un numéro (un entier strictement positif). À partir du deuxième étage, le numéro d'un cube est égal à la somme des numéros des quatre cubes placés juste au-dessous de lui. Les numéros des cubes du premier étage sont tous différents.
1A. Quel est le numéro minimum du cube du quatrième étage ?
Le promoteur souhaite de plus que les numéros des trente cubes soient tous différents.
2A. Quel est alors le numéro minimum du cube du quatrième étage ?