Traditionnellement, un carré magique d'ordre n est constitué de n2 entiers écrits dans les cases d'un tableau n × n. Ces nombres sont disposés de telle sorte que leurs sommes sur chaque ligne, sur chaque colonne et sur chacune des deux diagonales principales soient toutes égales. Un carré magique est normal s'il est composé des entiers positifs de 1 à n2.
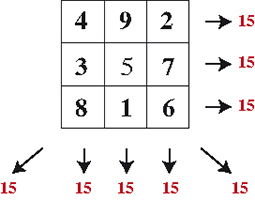
Le Lo Shu, carré magique
connu en Chine
bien avant notre ère.
Si l'on additionne case à case les nombres de deux carrés magiques du même ordre, le carré résultant est toujours magique, avec pour constante magique la somme de celles des deux carrés. Mais si les deux carrés additionnés étaient normaux, les nombres qui constituent le carré résultant ne sont en général pas tous distincts.
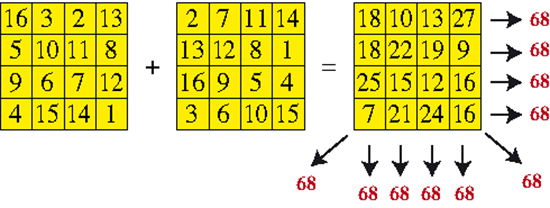
Les deux carrés normaux additionnés (de somme 34)
sont « de type associé » (les nombres placés symétriquement
par rapport au centre du carré sont complémentaires).
Cette propriété est conservée par l'addition.
On peut également multiplier tous les nombres d'un carré magique par un même nombre, entier naturel, entier relatif, rationnel ou réel. L'ensemble des carrés magiques d'ordre n est un sous-ensemble de l'ensemble des matrices carrées n × n. Si les coefficients du carré magique sont des entiers relatifs, l'ensemble des carrés magiques d'ordre n muni de l'addition case à case et de la multiplication par les entiers relatifs a une structure de module sur l'anneau des entiers relatifs.
L'ensemble des matrices carrées magiques n × n à coefficients réels, muni de l'addition case à case et de la multiplication par un réel, a, lui, une structure d'espace vectoriel. C'est un sous-espace de l'ensemble des matrices carrées n × n. Sa dimension est égale à n (n – 2). Pour l'ordre 3, on a donc un espace vectoriel de dimension 3. Voici une base possible de cet espace vectoriel.
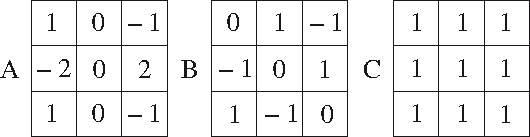
Avec les carrés A et B, on peut construire tous les carrés
de somme magique nulle, le carré C permettant d'ajuster
la constante magique à une valeur donnée.
1. Écrivez le Lo Shu comme une combinaison linéaire de ces trois carrés.
Pour les carrés d'ordre 4, la dimension est égale à 8. Vous en trouverez une base ci-dessous.
2. Écrivez le carré d'Albrecht Dürer (le premier carré jaune dans l'addition de deux carrés ci-contre, dont deux cases en bas indiquent sa date de création, 1514) comme une combinaison linéaire de ces huit carrés.
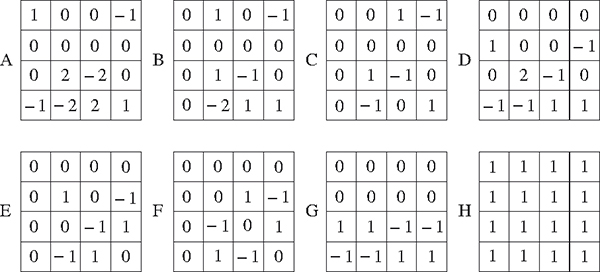
Les carrés A à G permettent de construire tous les carrés
de constante magique nulle, le carré H permettant d'ajuster
la constante magique à une valeur donnée.

