En 1635, le gouvernement du shogun, puissant seigneur féodal qui tenait alors en tutelle le mikado (empereur du Japon), interdit à tout Japonais de se rendre à l’étranger sous peine de mort. Quatre ans plus tard, en 1639, ce même gouvernement rompt toute relation avec le Portugal et l’Espagne, qui commerçaient depuis longtemps dans ces contrées. Seuls les Néerlandais et les Chinois furent autorisés à commercer avec le Japon, à condition que leurs navires accostent sur une île artificielle au large du port de Nagasaki. Pendant la majeure partie de la période qui suivit, désignée sous le nom de période Edo (1603–1867), le Japon vécut replié sur lui-même et coupé presque totalement du reste du monde. Les livres, et en particulier ceux de mathématiques, cessent alors d’entrer dans le pays.
Or une tradition existait alors : celle de réaliser des tablettes de bois peint, que l’on accrochait à l’intérieur des temples, en offrande aux dieux (la religion prédominante au Japon étant le shintoïsme). Certains dieux étaient supposés aimer particulièrement les chevaux ; on leur offrait alors des représentations de chevaux. D’autres étaient supposés aimer par dessus tout… les théorèmes de géométrie. C’est la raison pour laquelle des mathématiciens, mais aussi des gens de toutes conditions, paysans, lettrés, samouraïs…, se lancèrent dans la géométrie, et offrirent le fruit de leurs cogitations, sous la forme de tablettes représentant les résultats qu’ils avaient obtenus. Une tablette contenait le nom et la position sociale de son créateur, et un ou plusieurs théorèmes illustrés en couleur, généralement sans démonstration. Ces tablettes accompagnées de figures colorées très esthétiques sont désignées sous le nom de sangakus.

Une tablette de la préfecture de Fukushima.
Le problème proposé dans chaque tablette consistait généralement à établir une relation entre diverses grandeurs : rayons de cercles ou côtés de triangles ou de carrés. Mais on peut également se poser la question de la construction de ces figures, à la règle et au compas, même si elles n’ont probablement pas été construites de cette façon.
Trois disques et deux pentagones
Ce premier problème, qui apparaît sur une tablette de la province de Gumma, date de 1824. On y demande d’établir la relation entre les rayons des trois disques, R1 désignant le rayon du disque rouge, R2 celui du disque vert et R3 celui du disque jaune.
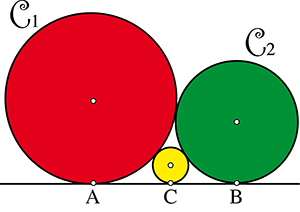
Pour établir cette égalité, il suffit d’exprimer les trois distances AC, CB et AB en utilisant les relations AC2 = 4R1R3, CB2 = 4R3R2 et AB2 = 4R1R2, que l’on obtient à l’aide du théorème de Pythagore.
1. Mais, en disposant de la droite (AB), des cercles C1 et C2 et de leurs centres, comment construire le petit cercle C3 en utilisant seulement la règle et le compas ?
Sur une autre tablette, deux pentagones réguliers ayant un côté commun sont inscrits dans un cercle. On inscrit un petit disque dans le triangle ABH et un second disque tangent à l’arc de cercle et aux côtés [ED] et [EF] des deux pentagones. On demande de prouver que le rayon du grand disque rouge est le double de celui du petit.
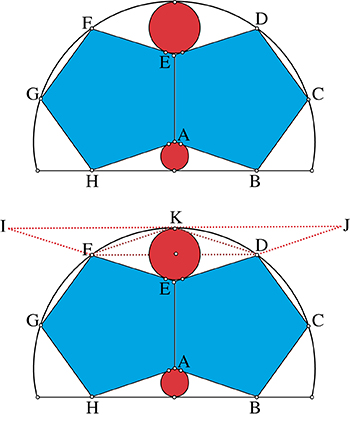
Pour démontrer cette relation entre les rayons des deux disques rouges, on utilise le fait que le triangle EIJ dans lequel est inscrit le plus grand des deux disques est semblable au triangle ABH, le rapport de similitude étant égal à 2.
2. Mais si l’on dispose du grand cercle et de son centre A, comment construire la figure ?

