
La réforme des mathématiques modernes des années 1960-1970 fut majeure et mondiale. On peut la comparer avec ce que fut la réforme du XVIIe siècle qui vit l'algèbre littérale, celle des polynômes et des équations, entrer dans les collèges et dans les universités. À peine quelques décennies plus tôt, la trigonométrie s'installait avec des tables numériques, confortées par l'invention du logarithme, qui avait été inconnu de la géométrie grecque. La fonction logarithme entraîna la conception des fonctions sinus, tangente…, qui auparavant étaient pensées comme des longueurs géométriquement repérées, sans intervention de la courbe sinusoïdale. Le véritable sens de cette réforme conceptuelle est l'invention de tables numériques : elles changent l'idée des mathématiques en ce que l'on doit apprendre à gérer l'approximation.

Portrait de mathématicien, par Ferdinand Bol (musée du Louvre).
Ces tables nouvelles, si utiles aux géodésiens, qui mesuraient ainsi les territoires coloniaux conquis, donnaient à l'homme européen l'impression de pouvoir ignorer toutes les mathématiques développées dans les pays hors d'Europe, et du monde plus ancien de l'Islam, qui restaient une influence reconnue.
La révolution du calcul intégral
Le mot « réforme » n'est pas équivalent au mot « révolution », trop aisément employé. Mais on peut l'utiliser pour la fin du XVIIe siècle, qui entraîna un investissement inouï, et inattendu, des mathématiques dans la conception que l'on avait de la cosmologie par la mécanique céleste, et du monde physique en général. La révolution fut le fait du calcul différentiel et intégral, qui n'avait qu'un maigre support géométrique (celui des tangentes), et sans grande garantie logique au sens de l'axiomatique euclidienne. Il acquérait une redoutable efficacité dans l'investigation abstraite des nouvelles fonctions, jusqu'au sinus auquel il donnait un développement en série entière, et donc renouvelait jusqu'à la procédure d'établissement des tables. En mathématiques élémentaires, celles de l'enseignement qui a besoin de normes, il y eut mise en place de nouveaux « rituels ».
La réforme du début du XVIIe siècle, par l'emploi des tables numériques, entraîna l'habitude des fractions et l'écriture, très différente, des nombres décimaux illimités. Cette écriture allait ensuite servir de modèle à l'une des réussites annexes de la révolution du calcul différentiel et intégral, à savoir les séries entières, dont le maniement était calqué sur la série géométrique 1 + x + x2 + x3 + … exprimant le nombre 1/(1 – x). On peut faire « voir » la démarche en exprimant que le calcul de a / (b – c), avec trois nombres positifs a, b et c, se fait à partir de la multiplication de a/b, évidemment avec c < b, grâce à la série 1 + (c /b) + (c /b) 2 + (c /b) 3 + … Ainsi disparut très lentement la pratique des proportions.
Le portrait ci-contre est dû à Ferdinand Bol, dans le dernier tiers du XVIIe siècle. Le mathématicien, non identifié mais qui pourrait être John Wallis, impose une calme résolution. Son compas de proportion est replié et, devenu baguette du maître, il désigne une figure géométrique tracée au tableau (une première en peinture !). La figure remplace les proportions par des tables numériques, qui ne sont pas figurées. Tracée en blanc comme à la craie sur un tableau, elle nous paraît banale : elle donne les lignes trigonométriques telles qu'on les expliquait dans le demi-cercle trigonométrique non orienté depuis la fin du XVIe siècle (le cosinus, le sinus, la tangente, la sécante). C'était une véritable réforme que de faire admettre ces lignes, en adjonction aux livres géométriques des Éléments d'Euclide ! Ces lignes n'avaient même pas eu accès aux livres dits « de géométrie pratique », qui s'occupaient de diverses constructions en se référant scrupuleusement aux préceptes euclidiens, jusque dans les démonstrations effectuées.
Science émergente, la trigonométrie n'est pas un prolongement de la géométrie pratique, et dérangera longtemps l'ordonnance de l'enseignement, avant que l'exponentielle complexe d'Euler et de d'Alembert ne la fasse apparaître comme une annexe facile, et un peu fastidieuse, de l'analyse mathématique. À l'époque, ces lignes étaient accompagnées de tables numériques, donc d'une pratique de mesure inconnue de l'enseignement universitaire d'alors. Elles étaient porteuses d'un concept difficile à naître, celui de fonction. Les formules de la trigonométrie sont bien là pour rappeler le cercle dans ce qui pourrait paraître ne concerner que le triangle rectangle.
Réforme normative : analyse et composition
Les réactions sont des aménagements professionnels des professeurs qui ont la charge bien difficile de ne pas présenter de la mathématique un visage désuni, alors que celles-ci connaissent des mutations. La jolie géométrie du triangle du XIXe siècle peut être vue comme une réaction à la géométrie analytique des manuels du XVIIIe siècle, elle-même étant une intelligente évolution par rapport à la géométrie algébrique issue de Descartes et Fermat.
Prenons le cas du mathématicien écossais Robert Leslie, qui, en 1822, voulait absolument présenter une démonstration géométrique élémentaire en deux parties successives, l'analyse et la synthèse, alors qu'il cherchait à inscrire un carré dans un triangle qu'il disait être quelconque. À cette époque, la proportion AF:AE::FG:EB, égale à dans une notation moderne, s'exprimait sans écriture symbolique depuis la tradition grecque : « AF est à AE comme FG est à EB. » Justement, Leslie réformait en partie l'écriture, sans pour autant accepter ce qui pouvait faire algèbre.
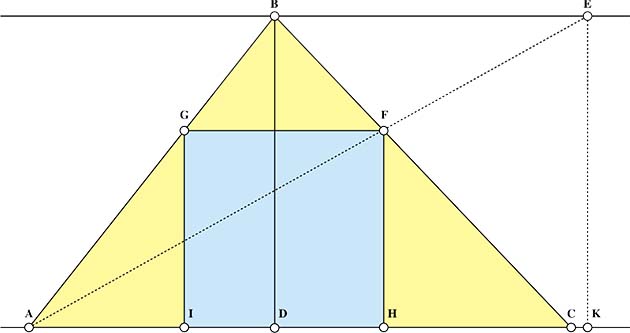
Construire un carré inscrit dans un triangle.
Proposition X. Soit un triangle ABC dans lequel il est demandé d'inscrire un carré IGFH.
Analyse
Joins A et F et prolonge la droite pour rencontrer en E une parallèle à AC [passant par B] et fais tomber les perpendiculaires BD et EK.
Parce que EB est parallèle à FG ou AC, AF:AE :: FG:EB (Éléments d'Euclide, VI, 2).
Et parce que la perpendiculaire EK est parallèle à FH, AF:AE::FH:EK.
D'où FG:EB::FH:EK. Mais FG = FH, et en conséquence (Éléments d'Euclide, V, 8 et 5), EB = EK. Et encore, EK étant égal à BD, la hauteur du triangle ABC est donnée, et donc EB est donnée à la fois en position et en grandeur, et en conséquence la parallèle FG et la perpendiculaire FH sont données, et donc le carré IGFH est donné.
Composition
De B, tire la perpendiculaire BD et tire BE parallèle à AC, fais BE égal à BD, joins AE, qui intersecte BC en F, et complète le rectangle IGFH.
Parce que BE et EK sont parallèles à GF et FH, AE:AF::EK:FH. Mais BE = EK, et en conséquence GF = FH. Il en est évident que IGFH est un carré.
Pour favoriser une « plus juste appréciation de la pratique [cultivation en anglais] des mathématiques », et pour préparer les esprits à la « philosophie inductive », Leslie restaurait en conscience « l'analyse géométrique » des Anciens, en prenant bien soin de ne citer qu'Euclide, et notamment de ne pas utiliser la forme en égalité de fractions des proportions. Sa réforme normative du raisonnement consiste à diviser un problème en deux parties distinctes, une partie d'analyse, et une autre partie qu'il appelait « de composition », car il ne voulait pas utiliser le mot trop usé de « synthèse ». D'où peut venir l'idée de la preuve de Leslie ? Il ne le dit pas, car sa « réforme » concerne la manière d'exposer les mathématiques, non de trouver du nouveau.
De la géométrie, en Chine et en Grèce
Les plus anciens témoignages sur l'inscription d'un carré dans un triangle sont celui de Héron d'Alexandrie (IIe siècle) et de Liu Hui en Chine dans son commentaire du IIIe siècle au livre les Neuf Chapitres sur les procédures mathématiques. Dans les deux cas, c'est une recette qui est donnée, pour le triangle isocèle chez Héron, pour le triangle rectangle chez Liu Hui. Les auteurs évoquent chaque fois le cas d'un angle obtus sur la base sur laquelle on veut construire. Le texte chinois peut être ainsi traduit.
Supposons que la base vaille 5 pas et la hauteur 12 pas. On demande combien vaut le côté du carré inscrit sur la base.
Réponse : le côté du carré vaut 3 pas et 9 / 17 de pas.
Procédure. On somme la base et la hauteur, ce qui fait le diviseur. On fait le produit de la base par la hauteur, ce qui fait le dividende. Et en effectuant la division du dividende par le diviseur, on obtient le côté du carré en pas.

Page extraite des Neuf Chapitres sur les procédures mathématiques.
La hauteur et la base peuvent être échangées sans que le résultat de la longueur du côté du carré inscrit ne varie. Seule la figure du triangle rectangle fait comprendre visuellement cette symétrie. Toutefois, les preuves de ces deux énoncés sont radicalement différentes ! La reconstitution possible suivante, « à la manière de » Héron d'Alexandrie, montrera la nécessité d'une réforme. Reprenons la figure de Leslie.
Supposant le carré construit. Par parallélisme de (GI) et (BD), GI est à BD comme AG à AB, donc par « division de raison » BD – GI est à BD comme AB – AG (soit GB) est à AB. Mais, par parallélisme de (GF) et (AC), GB est à AB comme GF est à AC. Donc la différence entre la hauteur et la longueur cherchée est à la hauteur comme la longueur cherchée est à la base.
Ce résultat suffit à déterminer la longueur cherchée pour un Grec de l'époque classique qui n'a pas l'idée d'une formule algébrique mais qui connaît la théorie des proportions. Cette théorie que nous avons, nous, oubliée, permettait de reconnaître que la longueur du côté du carré inscrit est le double de la moyenne harmonique de la hauteur et de la base ! La moyenne harmonique M de deux grandeurs h et b est, par définition, telle que son inverse est la moyenne arithmétique 1 /h + 1 /b des inverses de h et de b. Ou encore, M est la troisième proportionnelle entre la moyenne arithmétique et la moyenne géométrique, soit avec nos notations bh / (b + h). Il ne semble pas y avoir la moindre chance pour que la construction géométrique de la moyenne harmonique ait donné une construction du côté du carré inscrit autre que celle rapportée par Leslie. Pour obtenir une formulation de la longueur du carré en termes de proportion seulement, un double mouvement intellectuel est nécessaire : dépasser les proportions par un peu d'algèbre, puis revenir aux proportions. Il est possible de maintenir les proportions pour le cas du carré inscrit, mais à quel prix ! La preuve chinoise, quant à elle, est d'une tout autre nature. Ce qui intéresse les géomètres chinois, c'est l'expression de la longueur x d'un côté du carré, en fonction des longueurs dans un triangle rectangle (base b, hauteur h, hypoténuse H).
Le procédé chinois, comme celui du calcul de x par les proportions (algébrisées ou non), présuppose le problème résolu avant de pouvoir calculer et demontrer qu'il existe une, et une seule, solution. Il faudra attendre René Descartes pour voir apparaître le premier raisonnement qui certifie a priori que la méthode employée va effectivement conduire à une solution, et que cette solution sera unique. Dans La Géométrie (1637) en effet, il veut identifier des coefficients, dans le but de déterminer la tangente à une courbe donnée. Il considère alors un polynôme de degré 6, et explique a priori pourquoi des racines complexes ne pourront pas apparaître dans l'application de la méthode employée. A priori, la méthode des coefficients indéterminés résout le problème posé, on peut donc la mettre en œuvre !

René Descartes
L'exemple du carré inscrit dans un triangle donné a pu servir à al-Khwarizmi, non pour inventer l'algèbre (ce qui serait plus qu'une réforme !), mais pour illustrer la résolution par une équation. Ce faisant, il réforme une pratique de géométrie : il calcule l'aire du triangle de deux façons différentes (l'une par multiplication de la base par la hauteur et division par deux, l'autre en décomposant son triangle en trois petits triangles, AGI, BFG et FCH, et un carré, FGIH). La formule obtenue permet de trouver x car il y a disparition des termes en carré de x. C'est là la puissance de l'algèbre : cette simplification, prévisible (si l'on y songe seulement), fait que le résultat est déterminé, et non pas issu d'une équation du second degré qui risque d'avoir deux solutions. La disparition du carré est la traduction d'un problème linéaire.
La lecture du passé n'incite pas au relativisme
Au XVIe siècle, Jacques Peletier du Mans, qui commentait sa réforme d'Euclide sur un ton amusé, se réjouissait de voir que les différentes manières de présenter les mathématiques ne se contredisaient pas. Mais il fustigeait aussi les « furieux » de l'axiomatique :
« Ne s'en trouvera pas un seul [de ces principes géométriques] qui détruise, ni intéresse ni même combatte tant soit peu, ni les précédents, ni ceux qui suivent. Jamais aussi les membres de ce corps ne conspirent à la ruine l'un de l'autre, si ce n'est en quelque personne furieuse et maniaque. »
Les « maniaques » tiennent à un rituel plus qu'à une théorie. En cherchant à obtenir un texte unique et irréprochable, les mathématiciens ont dû constamment réformer les textes plus anciens, reprenant ce qui est déjà connu pour être plus clair. C'est vrai pour les Éléments : si Euclide a pu donner le ton axiomatique et irréel à bien des textes mathématiques après lui, son écrit a toujours été amélioré, repensé, modifié, même lorsque les historiens s'en emparèrent pour atteindre un Euclide originaire idéal. De même pour les Éléments de mathématique de Nicolas Bourbaki des années 1950, bâtis sur le même principe : il a fallu plusieurs fois renouveler le texte. Il y a quelque chose de paradoxal dans la volonté de réforme, alors que le texte en vue est à chaque fois pensé comme définitif. Les « mathématiques modernes », jugées outrancièrement réformatrices, sont entrées dans la norme traditionnelle, et les manuels qui ont eu cours dans les années 1970 furent révisés, modifiés… Se pose alors la question de l'intérêt qu'il y a à lire les textes anciens, et même récents, lorsqu'ils ont été remplacés par de nouvelles productions dans le but de les améliorer !
Il ne viendrait à personne l'idée de « réformer » des textes de Virgile ou d'Aristote, sauf à les simplifier en morceaux choisis. Faut-il imaginer un tel sort pour les textes mathématiques ? Lire le morceau de Leslie a au moins contribué à forger l'esprit critique.
Propos recueillis par É. T.
 Ce texte est issu de la conférence donnée par Jean Dhombres le mercredi 14 janvier 2015 à la Bibliothèque nationale de France dans le cadre du cycle « Un texte, un mathématicien ».
Ce texte est issu de la conférence donnée par Jean Dhombres le mercredi 14 janvier 2015 à la Bibliothèque nationale de France dans le cadre du cycle « Un texte, un mathématicien ».
La manie de réforme
Quelles sont les raisons qui font changer ? Aller contre la volonté de stabilité des programmes de tous les niveaux (qui sont définis nationalement par des commissions d'enseignants mathématiciens) en est une. Le choix dans les mathématiques diffusées dépend en plus des valeurs qu'une société attribue à la formation par l'enseignement même des mathématiques : esprit logique, capacité d'imagination et de synthèse, habileté au calcul et capacité d'analyse, préparation à la modélisation, sens de la certitude, objectivité, neutralité scientifique… Sans oublier les raisons économiques : besoin de formation d'ingénieurs, où l'on peut estimer que telle mathématique sera préférable à une autre… Les mathématiques que l'on enseigne et que l'on pratique relèvent d'un choix et impliquent des « rituels ».
La présentation euclidienne n'est pas la mise à disposition de tout ce qui était connu du temps d'Euclide, après l'âge d'or de la science grecque (IVe siècle avant notre ère). Pas plus que Bourbaki ne présente l'état des mathématiques de 1950.
