
Le mathématicien norvégien Atle Selberg.
Traditionnellement, les nombres premiers sont définis comme les nombres sans diviseur autre qu'eux-mêmes et l'unité. Pour éviter d'y inclure le nombre 1, de nos jours, cette définition s'écrit souvent de la façon suivante : un nombre premier est un entier ayant exactement deux diviseurs.
Dans l'Antiquité, Ératosthène (276-194 avant notre ère) a montré comment déterminer les nombres premiers inférieurs à un nombre donné, en éliminant tous ceux qui ne le sont pas (voir Tangente 149). Par exemple, pour connaître la table de tous les nombres premiers inférieurs à 150, on commence par dresser la table de tous les nombres de 2 à 150. On garde 2, qui est premier, et on supprime ses multiples, ce qui ne demande aucun calcul : il suffit en effet de se déplacer de deux en deux dans la table. On recommence avec le premier nombre non supprimé, c'est-à-dire 3, en opérant de même, et ainsi de suite. On obtient le tableau ci-dessous.
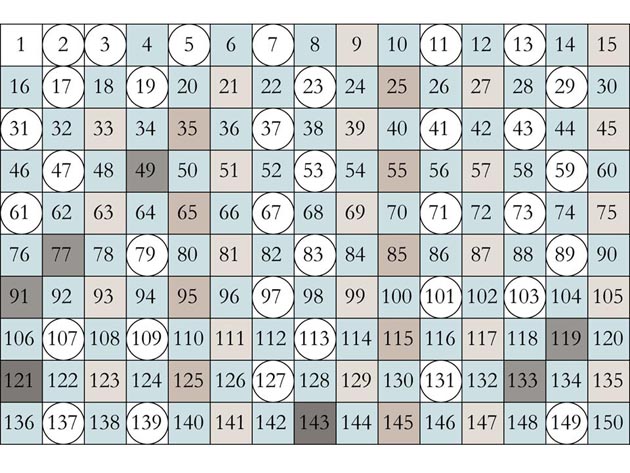
Crible d'Ératosthène : les multiples de 2 sont teintés en bleu clair, ceux de 3, 5, 7 et 11 sont en couleurs de plus en plus foncées. Les nombres premiers, repérés par des cercles, restent en blanc.
Limpide, simple et si belle…
La construction d'Ératosthène montre que tout nombre possède au moins un ... Lire la suite
