Une opération sur les complexes transforme les droites en cercles et inversement. Une transformation à garder en tête pour traiter des problèmes de droites et de cercles…
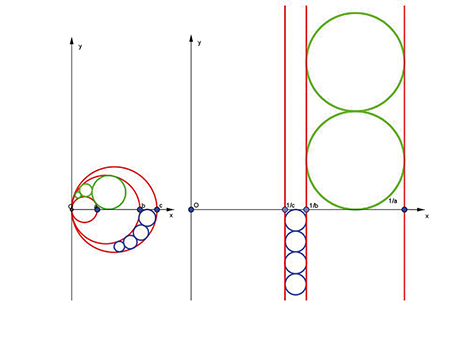
Les opérations sur les nombres complexes z d'image M et z' d'image M' trouvent toutes leur interprétation géométrique : à l'addition z + z' la somme vectorielle 
à la soustraction z – z' le vecteur 
, à la multiplication zz' l'image P telle que OP soit le produit des modules de z et z' et l'angle  )
soit la somme de leurs arguments. Mais pour la division ? Par exemple, le passage à l'inverse ? Dans cette transformation, qui à z associe z' = 1/z, l'argument de z' est l'opposé de celui de z et le module de z' est l'inverse de celui de z, si z est non nul. Cette jolie transformation, où le point O n'a pas d'image, transforme tout cercle passant par l'origine en une droite qui ne passe pas par O, tout cercle ne passant pas par O en un cercle qui ne passe pas par O, et réciproquement, tout en conservant les contacts, si bien que la figure de droite est l'image de la figure de gauche (et inversement).
Transformer des cercles en droites et réciproquement.
Lire la suite gratuitement
