Des points, des traits : en avant pour la fête des maths !

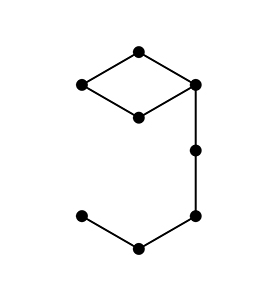
Difficile de savoir quand les maths vont vous prendre. Tout peut commencer très simplement, par exemple à la suite d’un long appel téléphonique à une administration peu disponible. Inconsciemment, vous attrapez un stylo pendant les diffusions en boucle d’un air de Vivaldi et vous commencez à griffonner un dessin. Vous pourriez par exemple obtenir le dessin ci-contre.

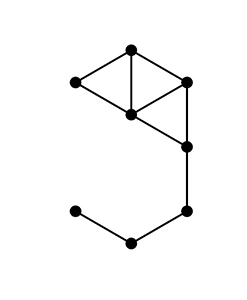
Sur votre bloc-notes, à côté du téléphone.	Dessin complété avec deux nouveaux segments de même longueur.

Vous avez placé huit points et matérialisé huit segments parmi tous ceux pouvant relier ces points. La forme de « neuf » est en apparence anodine mais une particularité vous frappe : tous les segments tracés sont de la même longueur ! Une fois le téléphone reposé, vous complétez avidement le dessin en rajoutant deux autres segments, toujours de la même longueur, dont un dans la boucle du « neuf », puis vous constatez que vous ne pouvez pas en ajouter d’autres sans ajouter de nouveaux points.

Un maximum de traits !

Une question mathématique naturelle s’impose : en fixant le nombre n de points, combien peut-on, au maximum, tracer de segments de la même longueur reliant ces n points (placés à votre guise et de manière astucieuse) ?

Pour n = 3, le problème est facile : le triangle équilatéral fournit une configuration où tous les segments traçables sont de la même longueur.

Pour n = 4, la figure carrée fournit quatre segments de même longueur (les côtés), mais on remarque vite que l’on peut faire mieux et obtenir cinq segments de même longueur en accolant deux triangles équilatéraux selon l’un de leurs côtés. Un raisonnement géométrique permet ensuite d’établir que l’on ne peut avoir six segments de même longueur reliant quatre points (et c’est un petit défi laissé à la sagacité des lecteurs).

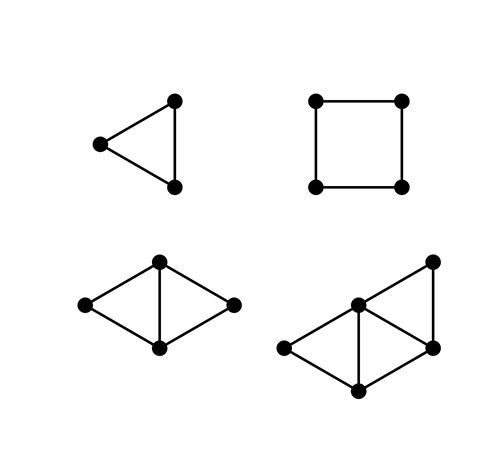
Des essais pour des petits nombres de points.

Pour n = 5, on peut obtenir sept segments de même longueur en rajoutant un triangle équilatéral contre l’un des côtés extérieurs, mais ne peut-on pas faire mieux en étant plus malin ?

Tandis que vous réalisez des tentatives de dessins avec des nombres de points un peu plus grands, vous parvenez à calculer quelques valeurs optimales pour de petites valeurs de n. Vous vous demandez ce qui se passe lorsque n devient vraiment grand. En d’autres termes, à quelle vitesse le nombre maximal de segments de même longueur évolue-t-il quand on fait varier le nombre de points ? Ce faisant, et sans le savoir, vous redécouvrez une conjecture de l’illustre mathématicien hongrois Paul Erd?s sur l’estimation asymptotique de cette quantité !

Erd?s avait en effet annoncé dans un très court article de 1946 qu’il « semblait probable » que le nombre de segments soit asymptotiquement plus petit que n^a pour tout a > 1. Il offrait même, comme à son habitude, une récompense de cinq cents dollars à quiconque serait capable de prouver ou d’infirmer cette conjecture ! Signe que le résultat doit être important pour les mathématiciens, cette prime est l’une des plus généreuses qu’il ait proposées.

Cette affirmation issue de l’intuition d’Erd?s est aujourd’hui encore une question ouverte. Le meilleur résultat dont on dispose date de… 1984 : le nombre maximal de segments est asymptotiquement dominé par n^4/3. C’est un beau résultat obtenu par les mathématiciens Joel Spencer, Endre Szemerédi (par ailleurs prix Abel 2012) et William Trotter. La preuve fut améliorée par Lazlo Székely en 1997, mais gardons bien en tête qu’il reste beaucoup de valeurs possibles pour l’exposant a entre 1 et 4/3. La conjecture de Erd?s tient toujours…

Et avec des traits prédéfinis ?

Comme souvent quand on s’intéresse à des questions sur les graphes, on peut regarder du côté du graphe de Petersen. On le mémorise facilement tant il semble issu d’un rituel satanique. Plus sérieusement, il s’avère être un redoutable contre-exemple pour de nombreuses intuitions mathématiques.

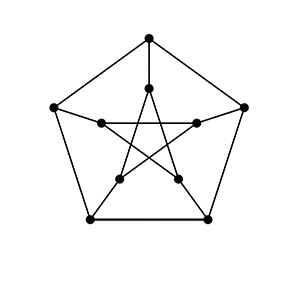
Le graphe de Petersen et son allure satanique.

Au regard de notre préoccupation, il semble en revanche fort décevant : les segments ne sont pas tous de la même longueur, même si ceux du pentagone central le sont. Toutefois, on remarque qu’en tournant judicieusement les points extérieurs et en « étirant un peu » la figure, on réussit à rendre tous les segments de même longueur ! On modifie le schéma, mais on conserve les segments qui reliaient les points : ceux-ci restent « attachés », « reliés » lorsque les points bougent. On obtient ainsi une autre représentation du graphe de Petersen, qui jouit cette fois-ci de la propriété recherchée.

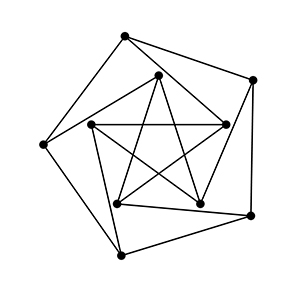
Une autre représentation du graphe
de Petersen. Cette fois-ci, tous les segments sont de même longueur.

En termes savants, on appelle graphe distance-unité un graphe qui admet un dessin avec tous les segments de même longueur. Voici une seconde question mathématique en apparence anodine : est-ce que tous les graphes sont distance-unité ? Autrement dit, est-ce que, pour tout dessin de graphe, il existe un déplacement des points qui rende tous les segments tracés de même longueur ? La réponse est négative et vous le savez déjà si vous avez relevé le petit défi du début. En effet, avec quatre points, on peut réaliser au plus cinq segments de même longueur ; par conséquent, en prenant quatre points et en les reliant avec six segments (c’est-à-dire en traçant tous les segments possibles), on obtient un graphe qui, même après déplacements des points, aura toujours deux segments de longueurs différentes.

Modifions alors la question : comment reconnaître les graphes distance-unité ? Le problème est plutôt difficile, voire très difficile. Pour vous en convaincre, regardez ce graphe très particulier, dit graphe de Heawood.

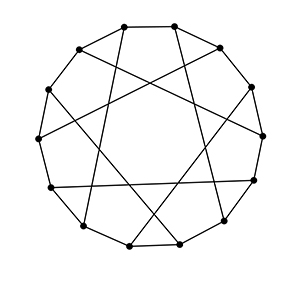
Le graphe de Heawood avec ses quatorze points et vingt et un segments.

Sur ce schéma, tous les segments ne sont pas de la même longueur. C’est une propriété facile à vérifier. Par contre, bien malin sera celui qui saura dire s’il existe une représentation du graphe de Heawood dont tous les segments sont de même longueur ! Trouver une représentation adaptée est difficile mais vérifier qu’une représentation est adaptée est facile. En 2013, le mathématicien allemand Marcus Schaefer a établi que ce problème était NP-complet, c’est-à-dire grosso modo qu’il appartient à la classe des problèmes (équivalents) considérés comme de grande difficulté à résoudre mais pour lesquels il existe des vérifications simples des solutions.

Cela dit, on peut montrer que le graphe de Heawood est bel et bien un graphe distance-unité.

On peut également expliquer comment discerner les graphes qui ne sont pas distance-unité à partir de l’exemple de quatre points dans le plan. Il est impossible de construire un dessin où les six segments sont de même longueur ; ce n’est pas tout à fait vrai, ou plutôt c’est vrai dans le plan. Si l’on fait un dessin en trois dimensions cette fois, alors il est facile de construire un tétraèdre régulier dont tous les côtés sont de même longueur !

Pour un graphe quelconque, trois dimensions ne suffisent pas toujours et on introduit la notion de dimension minimale de l’espace dans lequel le graphe admet une représentation dont tous les segments sont de même longueur (voir en encadré). Nous partions d’un dessin griffonné pendant une attente téléphonique et nous voici projetés dans la quatrième dimension ou au-delà ! Décidément, on ne sait jamais quand les mathématiques vont nous prendre…