Selon la légende, la princesse phénicienne Didon débarqua sur le site de l’actuelle Carthage vers 800 avant notre ère. Les habitants acceptèrent de lui céder autant de terrain que la peau d’un bœuf pourrait en englober. L’astucieuse princesse coupa alors la peau en fines lanières, pour en faire une longue corde qu’elle déposa en cercle pour maximiser l’aire du terrain englobé (ou peut-être un demi-cercle, bordé par le rivage…). On parle de problème isopérimétrique : le périmètre d’une courbe étant donné, déterminer ce que doit être cette courbe pour qu’elle englobe la plus grande aire possible.
La question se généralise à la dimension supérieure : pour une surface extérieure donnée, le volume maximal possible est celui d’une sphère. C’est une manière d’expliquer la forme sphérique d’une bulle de savon : le film tend à minimiser son énergie, elle-même fonction de sa surface.

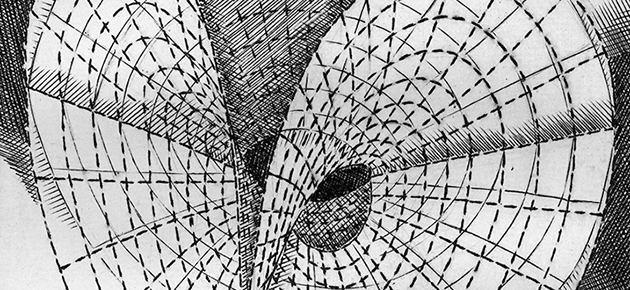
Surface obtenue expérimentalement en trempant deux cercles accolés dans de l’eau savonneuse, puis en perçant la bulle centrale, avant d’écarter les deux cercles.
Le statut particulier de la sphère
Si la sphère est minimale sous cet aspect, la reine des objets géométriques n’est pourtant pas considérée comme une surface minimale. Le terme est en effet réservé aux ... Lire la suite
