
L’origami et, plus généralement, les techniques de pliage d’une feuille de papier donnent lieu à de belles excursions dans le monde de la géométrie, de la topologie et de la combinatoire (voir notre dossier « La mathématique du pliage » dans Tangente 146, 2012). Si l’on enrichit la panoplie des opérations permises, par exemple en s’autorisant à couper la feuille de papier, quelles perspectives nouvelles s’ouvrent ? Le cas des cartes animées (ou pop-ups en anglais) est à lui seul déjà riche d’enseignement et offre des pistes de recherche originales et abordables pour tous les amateurs de belle géométrie.
Heaume sweet heaume
L’ingénieure Stephanie Jakus et le mathématicien Joseph O’Rourke se sont intéressés à une carte particulière. Avant de démarrer, il convient de savoir faire la distinction entre un pli vallée et un pli montagne. Dans le premier cas, la droite portant le pli peut servir de support (instable) à la feuille ; on le note schématiquement avec une ligne discontinue. Dans le second cas, le pli forme une crête ; on note avec une alternance de traits et de points.
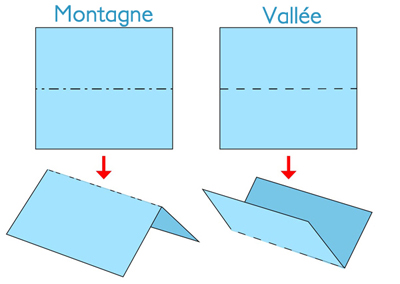
Le pli vallée et le pli montagne.
Pour construire la carte de Jakus et O’Rourke, on commence par plier la carte en deux volets à ... Lire la suite
