Les séries de fonctions ont pris leur essor au XVIIIe siècle, mais ce n’est qu’au siècle suivant que des théorèmes précis ont permis de connaître leurs propriétés, en particulier d’étudier leur continuité et leur dérivabilité. Cela a permis d’étendre considérablement le nombre de fonctions mathématiques, au lieu de se restreindre à des combinaisons d’opérations algébriques sur des fonctions élémentaires comme les puissances, les racines, le logarithme, l’exponentielle ou les fonctions trigonométriques. En particulier, de nombreux exemples de fonctions qui défient l’intuition ont pu être ainsi exhibés.
Quand la somme est discontinue
On connaît l’illusion d’optique, illustrée par Maurits Cornelis Escher, d’une fontaine dont l’eau semble toujours couler et qui se retrouve… à son point de départ.
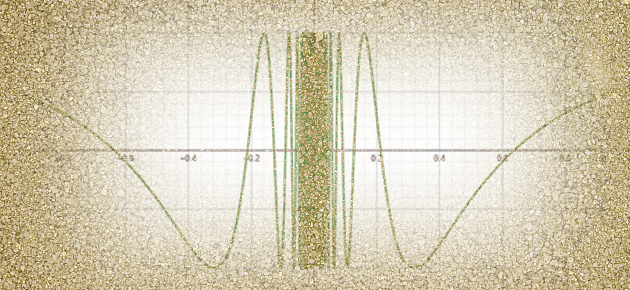
Voici un exemple de fonction périodique, continue en tout point irrationnel mais admettant un saut négatif en tout point rationnel (c’est-à-dire que la limite à droite en ces points est toujours strictement inférieure à la limite à gauche). Une fonction périodique qui décroît toujours ? L’intuition en prend un coup…
Notons E(x) la partie entière du nombre réel x et h (x) la différence x – E(x). Cette fonction (appelée partie fractionnaire et souvent notée {x}) est périodique puisque E(x+1) = ... Lire la suite
