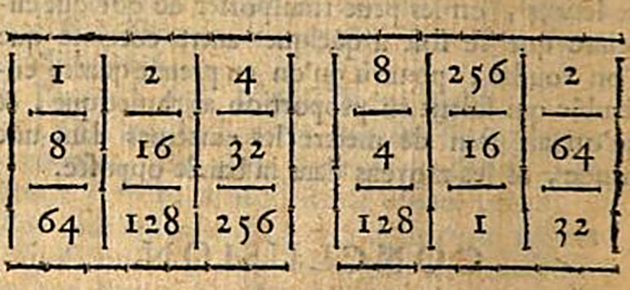
Le premier carré magique multiplicatif semble avoir été publié par le théologien et mathématicien Antoine Arnauld (1612–1694) dans ses Nouveaux Éléments de géométrie (1683).
Cet objet a été construit à partir du carré additif 3 × 3 (le Lo-shu, connu en Chine depuis plus de vingt-deux siècles). En effet, grâce à l’additivité des exposants, lorsque l’on multiplie des puissances d’un même nombre entre elles, la magie additive est conservée lorsque l’on remplace les nombres du carré additif par des puissances d’un même entier ayant pour exposants les nombres de ce carré initial. On obtient alors un carré multiplicatif, de produit magique 215, soit 32 768. Mais en diminuant tous les exposants de 1 (ce qui revient à partir d’un carré additif contenant les nombres de 0 à 8, au lieu des entiers de 1 à 9), Arnauld obtient un produit magique égal à 212, soit 4 096.

Le Lo-shu.

Le carré multiplicatif 3 × 3 obtenu à partir du Lo-shu.
Avec la seule contrainte d’utiliser des entiers tous différents, ce produit magique est loin d’être le plus petit possible ! En 1893, Georges Pfeffermann (1838–1914) publie, sous la forme d’une grille à compléter, un carré multiplicatif de produit magique 216. Cette valeur est la ... Lire la suite
