En 1936, Soddy publie un article, dans la revue Nature Magazine, consacré à une question de géométrie (voir Mathématiques et Chimie, Bibliothèque Tangente 43, 2012). Le problème est le suivant : si trois cercles sont tangents extérieurement deux à deux, on peut toujours en trouver un quatrième qui soit tangent à ces trois cercles. Dans le cas général, on peut même en trouver deux, les trois cercles étant tangents extérieurement à l’une des solutions, et intérieurement à l’autre.
1. Dans quel cas n’a-t-on qu’une solution ?
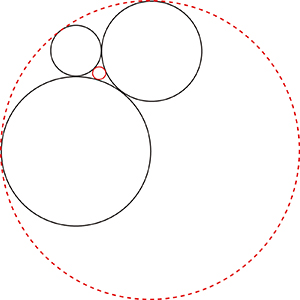
Quelle relation lie les rayons de quatre cercles tous tangents entre eux ? Une formule fut trouvée par Soddy. Si a, b et c désignent les rayons des trois cercles initiaux et r le rayon d’une des deux solutions, alors on a la relation suivante :

Cette relation avait déjà été formulée en 1643 par René Descartes dans une lettre adressée à la princesse Élisabeth de Bohème.
L’originalité de l’article de Soddy est qu’il n’a pas été rédigé comme un texte mathématique, mais sous la forme ... Lire la suite
