
Prenons une forme géométrique, un carré par exemple, et agrandissons-la. On obtient une forme proportionnelle. On dit aussi semblable. Cela signifie deux choses. D’une part que les proportions entre les différentes parties de la première figure seront les mêmes entre les parties correspondantes de la seconde figure.
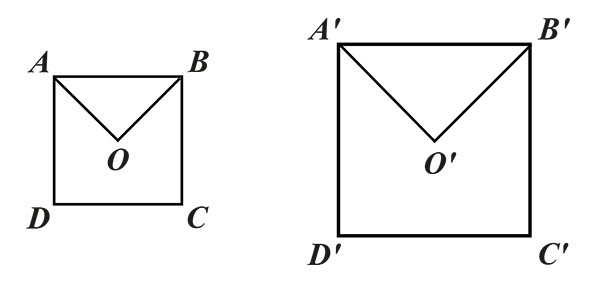
Ainsi, quand on a alors
Et si aire (AOB) = aire (ABCD) /4
alors on a aire (A'O' B' ) = aire (A' B' C' D' ) /4.
La forme étant conservée, cela signifie également que toutes les longueurs de la première figure vont être multipliées par un même nombre pour obtenir la seconde figure, par exemple par 1,5 dans le cas d’une augmentation de 50 %. Ce nombre est le coefficient de proportionnalité, la raison comme on disait dans l’Antiquité. La prise en compte de ce coefficient dépend de la nature des éléments que l’on va agrandir. Ainsi, si les longueurs sont multipliées par 1,5, les aires, elles, sont alors multipliées par 1,52 = 2,25 (soit une augmentation de 125 %) et les volumes par (1,5)3. On perçoit bien les pièges de communication associés à ces diverses possibilités d’interprétation quand on ne précise pas la nature de ce qui augmente.
La géométrie a ses raisons
Dans l’Antiquité, on utilise ... Lire la suite
