
L’arbelos fait partie de ces formes mathématiques facilement reconnaissables et qui ont suscité la curiosité de nombreux géomètres. Le mathématicien danois Jørgen Mohr (1640‒1697) a contribué à en relancer l’étude au XVIIe siècle avec son tricercle, menant plus récemment à des constructions étonnantes comme le parbelos, le f-belos et l’hyperbelos (figures semblables à l’arbelos, où les demi-cercles sont remplacés successivement par des arcs de parabole, ceux de la courbe représentative d’une fonction f ou ceux d’une hyperbole). Concentrons-nous ici uniquement sur les résultats d’Archimède, son inventeur, et son développement par Pappus d’Alexandrie (vers 290, vers 350).
Le tricercle de Mohr.
L’histoire d’une forme
Comme souvent avec les textes mathématiques grecs, tout commence par des doutes. L’opuscule où l’arbelos est décrit s’intitule Le Livre des lemmes, dont le titre indique qu’on y trouvera des résultats élégants et sympathiques et non des développements ambitieux. Si ce livre est attribué à Archimède, son authenticité est douteuse : les résultats sont peut-être de lui mais la manière assez désordonnée dont l’opuscule est rédigé ne ressemble pas au génie de Syracuse. Qui plus est, l’original grec est perdu. Fort heureusement, il nous est parvenu dans la traduction arabe qu’en a faite Thabit ibn Qurra au IX e siècle, lui qui est resté célèbre pour les « nombres de Thabit » et à qui l’on doit aussi de nombreuses traductions (Euclide, Ptolémée, Apollonius). Autant de traductions qui faisaient partie du programme de la Maison de la sagesse de Bagdad (voir Tangente 139, 2011).

« Arbelos » signifie en grec « couteau » ou « tranchet du cordonnier »
à cause de sa ressemblance avec la lame d’un couteau utilisé
par les anciens cordonniers, et dans le métier du cuir en général.
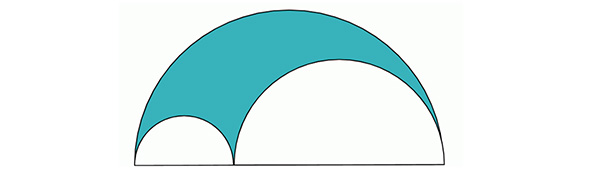
Archimède – pour dénommer simplement l’auteur sans doute collectif – a proposé dans cet opuscule une surface géométrique innovante, déduite de la différence entre un grand demi-cercle et deux petits demi-cercles tangents entre eux qui lui sont également tangents intérieurement. Cette forme, c’est l’arbelos, ainsi nommée en référence au couteau de savetier, formé d’un manche et, surtout, d’une lame en demi-lune très similaire à l’arbelos dans le cas de deux petits demi-cercles de même diamètre.
L’arbelos.
L’une des premières questions que se pose Archimède est de quarrer l’arbelos : connaître la surface d’une forme est un problème systématique dans les mathématiques grecques. Pour ce faire, en plus des demi-cercles de diamètre [AC], [AD] et [DC] (en conservant les notations de l’opuscule), il propose de s’intéresser au segment [BD] tangent aux deux petits demi-cercles.

Archimède (vers —287, —212)
tel que représenté par Raoul Dufy en 1937 dans La Fée électricité.
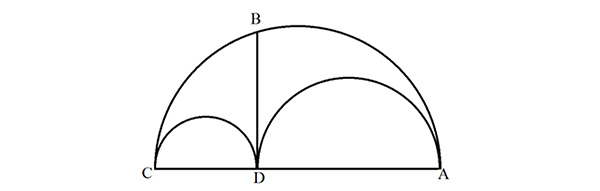
Les éléments géométriques utiles.
Le triangle ABC est rectangle en B (parce qu’il est inscrit dans un demi-cercle) et le segment [BD] est la hauteur à l’angle droit. Ainsi, BD est la moyenne géométrique de AD et DC, résultat qui se déduit rapidement de l’application du théorème de Pythagore dans les triangles rectangles ABD, BCD et ABC (propriété connue car elle apparaît chez Euclide, dans les Éléments). En termes géométriques (c’est ainsi qu’Archimède s’exprime), le rectangle formé sur [CD] et [DA] a la même surface que le carré formé sur [BD] (en orange). En termes algébriques modernes, BD2 = CD×DA.
De cela, on peut déduire rapidement :
AC2 = 2BD2 + CD2 + DA2. Tel qu’Archimède l’exprime, cela signifie que, en termes de surface, le carré rouge est égal à la somme des carrés bleu et vert à laquelle on ajoute deux fois le carré orange.
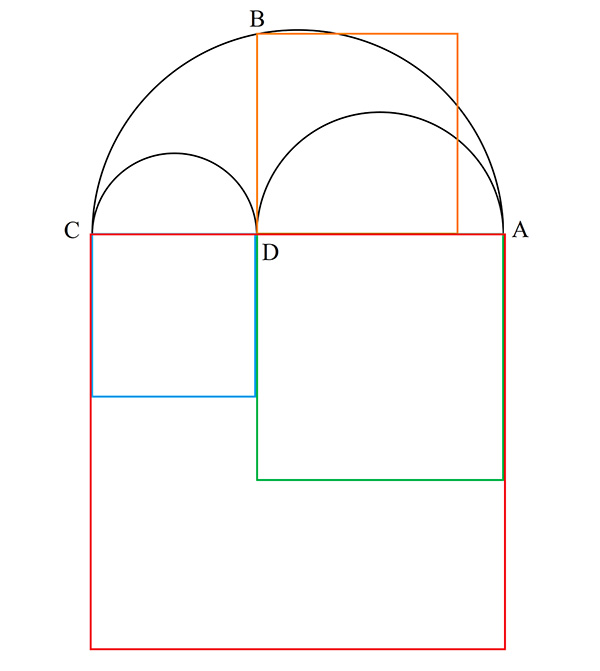
Quarrer l’arbelos.
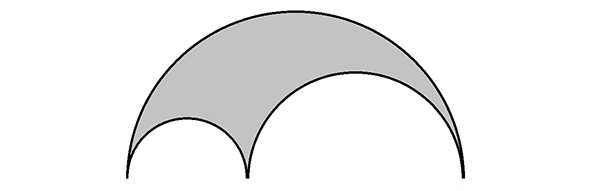
Or, le rapport des aires des cercles étant égal au rapport des carrés de leur diamètre (comme nous l’enseigne Euclide), ce qui précède, et qui vaut pour les carrés, vaut également pour les cercles de diamètres correspondants. Si l’on retranche du disque formé sur [AC] les disques formés sur [CD] et sur [DA], on obtient le double de la surface du disque formé sur [BD]. Puisqu’on ne s’intéresse qu’à la partie supérieure des trois premiers disques, on en conclut que l’aire de l’arbelos, qui est la différence de surface entre les trois demi-cercles, est égale à la surface du cercle formé sur [BD].
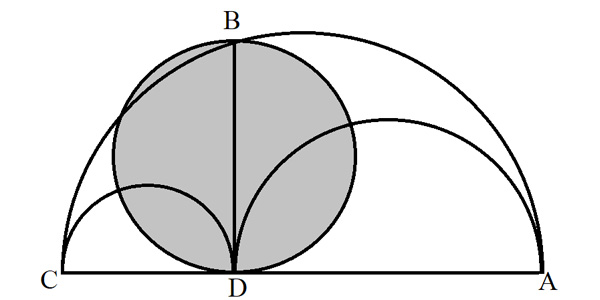
L’aire de l’arbelos est celle du cercle grisé.
Un nouveau cercletangent aux trois autres
Archimède se pose ensuite une autre question : quelles seraient les propriétés d’un cercle qui serait tangent aux trois demi-cercles précédents ?
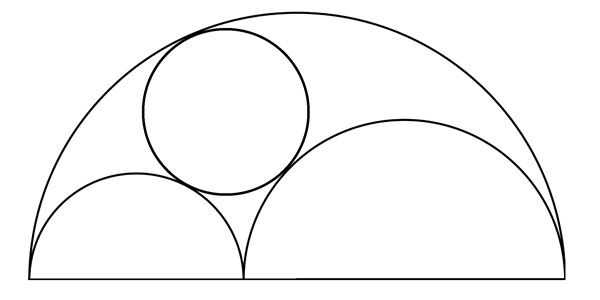
Quatre cercles tangents deux à deux.
Ayant toujours la perspective de la quadrature, Archimède se demande donc quelle serait la valeur du rayon de ce cercle. Pour trouver la réponse, il faut commencer par un lemme – d’où le titre de l’opuscule – qui établit un résultat sur les rayons de cercles tangents.
Archimède étudie la situation de deux cercles tangents intérieurement comme suit, dont on trace deux diamètres parallèles [AB] et [CD], le point de tangence étant E. Il s’occupe du cas où E est au point « le plus haut » du cercle de diamètre [AB], ce que l’on généralise ici. On peut montrer que les points E, D et B d’une part, et E, C et A d’autre part, sont alignés.
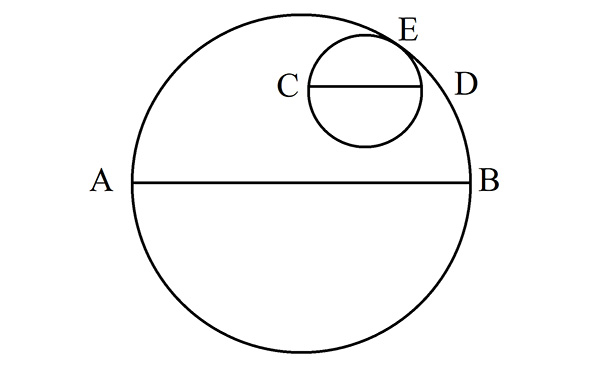
Alignements E, D, B et E, C, A.
Concernant E, D et B, on peut tracer les segments [EG] et [GF], G étant le milieu de [CD] et F celui de [AB], puis la droite (DH) parallèle à (GF). Ainsi, GD est égal à FH. Or, GD et GE étant des rayons du petit cercle, ils sont égaux.
Après avoir remarqué que les points F, G et E sont alignés avec FE = FG + GE (les cercles sont en effet tangents en E et la distance de leurs centres est égale à la différence de leurs rayons FE et GE), on cherche à évaluer l’angle
Puisque FE et FB sont égaux (en tant que rayons du grand cercle), on a :
HB = FB – FH (car F, H et B alignés)
= FE – GD (car GDHF est un parallélogramme)
= FE – GE = FG = HD.
Le triangle BDH est donc isocèle en H :
De plus, est égal à
(angles opposés d’un parallélogramme).
Or, les angles et
sont égaux car le triangle GED est isocèle en G (puisque [GE] et [GD] sont des rayons du petit cercle).
Ainsi, la somme est égale à
elle-même égale à 180° puisqu’il s’agit de la somme des trois angles du triangle EDG. Ce qui montre que E, D et B sont alignés.
Arbelos, les tracés intermédiaires.
On peut procéder de même pour A, C et E. Et on peut suivre un raisonnement similaire dans le cas où le cercle tangent est extérieur.
Le rayon du cercle tangent
On peut désormais calculer la valeur du diamètre [EF] du quatrième cercle tangent aux trois premiers (en reprenant à nouveau toutes les notations d’Archimède).
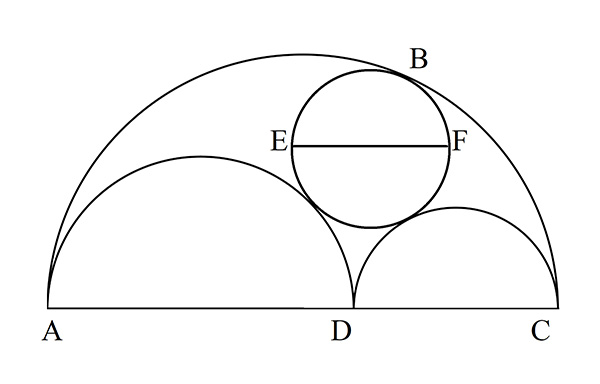
Rayon du cercle tangent : lemme.
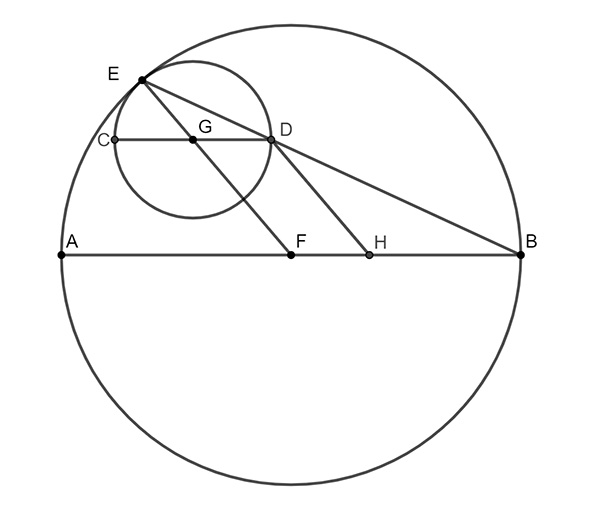
Grâce au lemme, on est en droit de tracer tous les segments possibles reliant points de tangence et extrémités de diamètre. Soit G le point de tangence entre le demi-cercle de diamètre [AD] et le cercle de diamètre [EF]. Soit H celui entre le demi-cercle de diamètre [DC] et le cercle de diamètre [EF]. Soient [EO] et [FP] perpendiculaires à [AC]. On place I sur [AE] tel que [DI] lui soit perpendiculaire en I, L sur [CF] tel que [DL] lui soit perpendiculaire en L ; M est le point commun à (AF) et (DI) et N à (CE) et (DL).
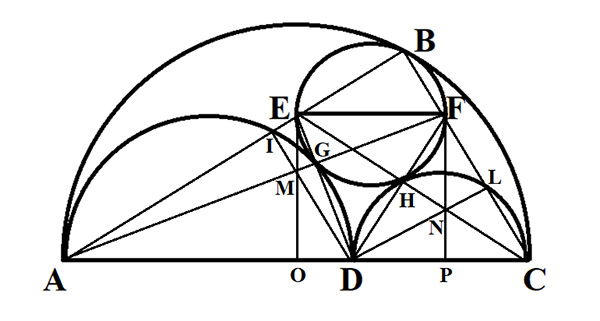
Rayon du cercle tangent : calcul.
On peut alors montrer que le point M, commun à (AG) et (DI), est aligné avec les points E et O. De même pour le point N, commun à (CH) et (DL), qui est aligné avec les points P et F. On en déduit que M et N se situent au croisement des hauteurs de leurs triangles respectifs. Ce qui permet de conclure que (AG) est une hauteur, et donc est perpendiculaire à (ED).
De même pour (FP) et (CA). On en tire alors comme conséquence que (DL) est parallèle à (AB) et que (ID) l’est à (BC).
On peut alors appliquer le théorème de Thalès pour obtenir, d’une part,
et, d’autre part,
Or, OP = EF et DC = AC ‒ AD,
d’où et
Il s’ensuit :
En posant
on peut enfin écrire
ce qui donne le diamètre du cercle tangent aux trois autres en fonction de la position de D sur [AC].
La chaîne de Pappus
Archimède propose d’autres résultats dans son opuscule, mais c’est chez Pappus (Collection, IV, 14) que l’on va trouver un aspect itératif de ce quatrième cercle : puisqu’on en a inséré un, pourquoi ne pas continuer indéfiniment ?
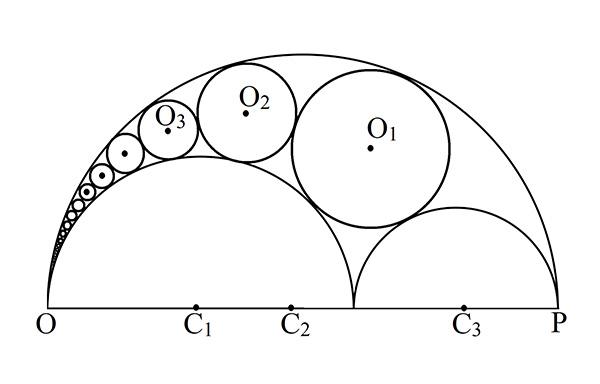
La chaîne de Pappus.
En notant d = OP le diamètre du grand demi-cercle, et dn celui du nème cercle inscrit, on peut montrer que la distance du centre On du nème cercle inscrit à la droite (OP) vaut hn = ndn.
Or, le diamètre du nème cercle inscrit vaut
ce qui est une fort jolie généralisation du cas étudié par Archimède. De plus, les points On appartiennent à l’ellipse de foyers C1 et C2 et de grand axe d ‒ C3P.
La chaîne de Pappus est un cas particulier qui ouvre sur d’autres questions comme les chaînes de Steiner et les badernes d’Apollonius. L’arbelos regorge ainsi de mille trésors dont on n’a fait que présenter ici quelques-uns de ceux que l’Antiquité a mis en évidence.
références
• Le livre des Lemmes. Archimède, in Œuvres, tome III, traduction Charles Mugler,
Les Belles Lettres, 2002.
•
Collection mathématique. Pappus d’Alexandrie, traduction Paul ver Eecke, Blanchard, 1933 (1982 pour la dernière édition).


