
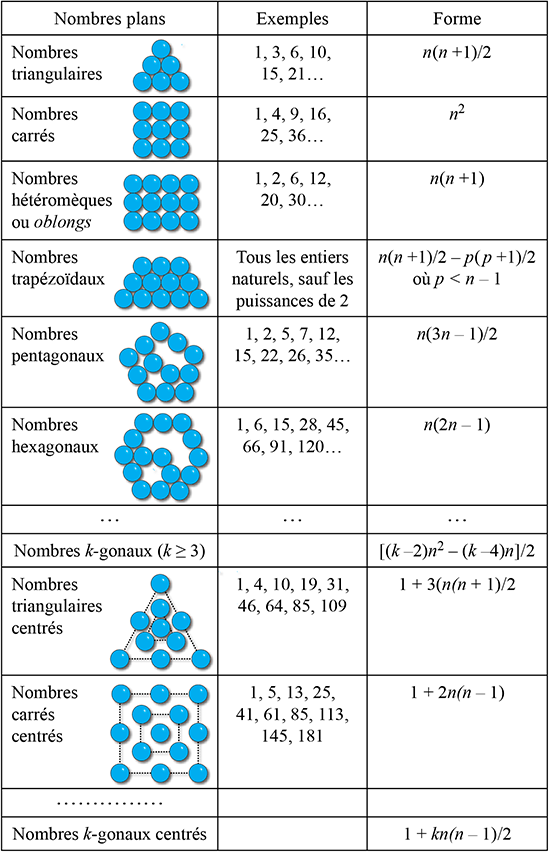
La fascination exercée par les nombres figurés (dont les propriétés sont rappelées dans les encadrés) a donné naissance à de nombreux problèmes arithmétiques. Beaucoup consistent à rechercher les entiers appartenant à deux classes distinctes de nombres figurés. Parmi les questions que l’on peut se poser, la plus séduisante est sans doute la suivante : les solutions sont-elles en nombre fini ou infini ?
Essayons de dresser un catalogue, partiel et partial, de ces problèmes. La diversité des types de nombres figurés permet d’en imaginer quantité d’autres. Avis aux amateurs !
Pensez à la récurrence !
Existe-t-il des nombres entiers qui soient à la fois carrés et triangulaires ?
La réponse est positive. Les premières solutions sont 0, 1, 36, 1 225, 41 616, 1 413 721, 48 024 900, 1 631 432 881, 55 420 693 056, 1 882 672 131 025… Elles sont liées par une relation de récurrence : si l’on note (an )n ≥ 0 la suite de ces entiers, on a a0 = 0, a1 = 1, pour n ≥ 2, an = 34 an–1 – an–2 + 2.
Existe-t-il des nombres entiers qui soient à la fois carrés et pentagonaux ?
La réponse est également positive. Les premières solutions sont 1, 9 801, 94 109 401, 903 638 458 801, 8 676 736 387 298 001… Elles sont elles aussi liées par une relation de récurrence : si l’on note (bn) n ≥ 0 la suite de ces entiers, on a b0 = 1, b1 = 9 801, pour n ≥ 2, bn = 9 602 bn–1 – bn–2 + 200.
Existe-t-il des nombres entiers qui soient à la fois carrés et hexagonaux ?
La réponse est encore positive. Les premières solutions sont 1, 1 225, 1 413 721, 1 631 432 881, 1 882 672 131 025, 2 172 602 007 770 041… Elles sont liées par une relation de récurrence : si l’on note (cn) n ≥ 0 la suite de ces entiers, on a c0 = 1, c1 = 1 225, pour n ≥ 2, cn = 1 154 cn–1 – cn–2 + 72.
On sait par ailleurs qu’il n’existe que trois nombres à la fois carrés et tétraédriques, à savoir 1, 4, et 19 600. Ce résultat a été démontré en 1878 par le mathématicien et capitaine d’artillerie néerlandais August Jan Franciscus Meyl.
Existe-t-il maintenant des nombres pyramidaux à base carrée qui soient aussi des carrés ?
Les entiers 1 et 4 900 répondent à la question et ce sont les seuls, comme le démontra le mathématicien britannique George Neville Watson (1886‒1965) en 1918.
Existe-t-il des nombres à la fois triangulaires et tétraédriques ?
La réponse est positive, mais il n’en existe que six : 0, 1, 10, 120, 1 540 et 7 140.
Enfin, existe-t-il des nombres à la fois triangulaires et pyramidaux à base carrée ?
Là encore, il n’y a qu’un nombre fini de solutions : 1, 55, 91, 208 335, et c’est tout !
Et avec les nombres premiers ?
Un autre type de questions chères aux « matheux » fait intervenir la notion de nombre premier. De fait, il est « naturel » de se demander quels sont les types d’entiers figurés pouvant contenir des nombres premiers.
On se rend immédiatement compte que seuls les nombres polygonaux de côté premier contiennent un, et un seul, nombre premier : 3 pour les triangulaires, 5 pour les pentagonaux, 7 pour les heptagonaux…
Les nombres polygonaux centrés (pour lesquels on compte en plus un pour le centre du polygone) sont plus prolifiques en nombres premiers.
On trouve ainsi :
• parmi les triangulaires centrés :
19, 31, 109, 199, 409, 571…
• parmi les carrés centrés :
5, 13, 41, 61, 113, 181, 313, 421, 613, 761…
• parmi les pentagonaux centrés :
31, 181, 331, 601…
Il y a toutefois des obstructions ! Les nombres octogonaux centrés, de la forme (2n +1)2, ne peuvent jamais être premiers. Il en est de même pour les nombres nonagonaux centrés, qui peuvent s’écrire (3n + 1)(3n + 2)/2.
De même, en raison de leur formule, on vérifie qu’aucun nombre pyramidal ne peut être premier. En revanche, certains nombres pyramidaux centrés peuvent compter un (et un seul) nombre premier : 5 pour la pyramide à base carrée, 7 pour la pyramide à base hexagonale, 11 pour la pyramide à base décagonale, 13 pour la pyramide à base dodécagonale…
Si les énigmes arithmétiques basées sur les nombres figurés vous intéressent, peut-être aurez-vous plaisir à revisiter le triangle de Pascal et ses innombrables propriétés. Un bon point de départ est alors notre dossier paru dans Tangente 176 (2017), ou encore notre hors-série 85 Blaise Pascal, paru en 2023 pour les 400 ans du célèbre mathématicien et philosophe clermontois. À défaut, pourquoi ne pas inventer vos propres énigmes et enrichir le catalogue des propriétés des nombres figurés ?
Les nombres plans : carte d’identité
Les nombres solides
.png)


