
Les Grecs de l’Antiquité avaient une numération alphabétique peu commode pour les calculs (α = 1, β = 2… ι = 10, κ = 20, ρ = 100, ς = 200…). Aussi s’aidaient-ils de petits jetons, qu’on appelle les psephoi. Ils pouvaient aussi bien servir pour l’abaque (comme les calculi, « petits cailloux », pour les Romains) que pour compter à même le sol ou sur une table. La chose la plus simple avec ces psephoi est de les aligner, à la manière dont un prisonnier fait des traits successifs sur les parois de sa geôle. Cela permet aussitôt de définir le nombre linéaire, première et plus évidente figuration des nombres, ainsi que le rappelle Boèce (Institution arithmétique, II, 4, 5, 1, texte établi et traduit par Jean-Yves Guillaumin, Les Belles Lettres, 2002) : « Le nombre linéaire est un entassement de quantité qui se déploie à partir de 2, si l’on ajoute toujours une unité sur une seule et même ligne, comme ci-dessous :
II III IIII IIIII IIIII IIIIII IIIIIII IIIIIIII IIIIIIIII. »
Bien sûr, si l’on en était resté là, les nombres figurés n’auraient pas eu le moindre succès. C’est l’étape suivante, consistant à passer des nombres linéaires aux nombres triangulaires, qui va marquer leur entrée dans la légende.
L’origine pythagoricienne
C’est à Pythagore que l’on attribue le plus célèbre des nombres figurés : la tetraktys. Il s’agit du nombre 10, écrit sous la forme d’un triangle équilatéral à dix points.

Comme le note l’auteur des Théologoumènes arithmétiques (écrits par un auteur qui se fait passer pour Jamblique), le nombre 10 est parfait pour plusieurs raisons : il contient autant de pairs que d’impairs, mais aussi autant de nombres premiers que non premiers (1 était considéré comme premier par les Grecs), et il est le plus petit entier à avoir une telle propriété. Surtout, 10 apparaît visuellement, grâce au dessin de la tetraktys, comme la somme 1 + 2 + 3 + 4.
Or, le rapport correspond à l’octave musicale. De même, le rapport
correspond à la quinte et le rapport
correspond à la quarte : ce sont les trois accords musicaux fondamentaux dont on attribue la découverte à Pythagore (même si en réalité, ce serait plutôt l’œuvre de Philolaos ou Archytas, disciples de l’école pythagoricienne). Ainsi, Jamblique (le vrai, cette fois !) explicite les différents symboles pythagoriciens dont « la tetraktys, c’est-à-dire l’harmonie, selon laquelle chantent les Sirènes » (Vie de Pythagore, 82).
Les sources antiques
Boèce, polymathe de la fin de l’Empire romain (vers 480–524), traduisit et adapta l’Introduction à l’arithmétique de Nicomaque de Gérase (IIe siècle de notre ère), arithméticien grec né en Jordanie actuelle, alors dans la partie orientale et hellénophone de ce même Empire romain. Ces deux auteurs font partie de la mouvance néopythagoricienne : six siècles après la mort de Pythagore (survenue autour de ‒500), sa pensée resurgit fortement, aussi bien en philosophie qu’en mathématiques. Boèce et Nicomaque en seront parmi les plus importants hérauts puisque Boèce sera lu en latin par l’Occident médiéval, et Nicomaque sera traduit du grec vers l’arabe dans le monde arabo-musulman. La dernière source importante concernant Pythagore (et, pour ce qui nous intéresse, la tetraktys) est Jamblique, lui aussi philosophe et mathématicien néopythagoricien.
La tetraktys est un exemple important d’une chose qui a disparu de la recherche arithmétique : l’arithmologie. Il s’agit d’une manière de chercher les propriétés philosophiques, symboliques voire magiques des nombres. C’est une approche très esthétique qui s’y développe, où l’on tente de mettre en évidence des résultats, non pas pour leur possible utilité mais pour leur pure beauté, laquelle nous montre l’incroyable ordonnancement des nombres, à la manière de l’étonnement qui fait naître toute philosophie.
De l’importance des triangles
En arithmologie, la méthode de construction est toujours itérative : on part du nombre figuré précédent pour former le suivant. La figure géométrique la plus élémentaire étant la ligne, on peut dans un premier temps aligner les psephoi les uns après les autres : on peut représenter tout nombre entier n comme un alignement de npsephoi. On obtient ainsi les nombres linéaires. Pour prendre un exemple, on notera le nombre 4 sous la forme P2,4 pour noter le quatrième nombre construit sur la forme géométrique nécessitant deux points, à savoir la ligne. Il sera représenté sous forme figurée ainsi :

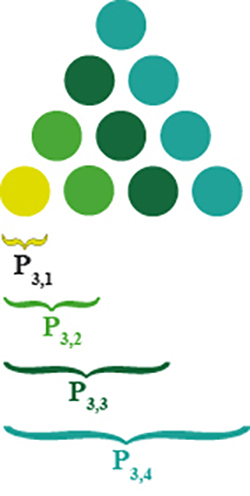
Après la ligne, qui nécessite deux points distincts, la forme géométrique directement plus élaborée est le triangle, qui nécessite trois points non alignés.
Le premier nombre triangulaire est un cas limite, comme pour tous les nombres figurés, puisqu’il correspond à un unique point à partir duquel on formera les triangles successifs.
Le deuxième nombre triangulaire s’obtient en adjoignant, à droite, deux autres points pour former un triangle équilatéral à trois points, que l’on notera P3,2 = 3.
Le suivant s’obtient de la même manière : en ajoutant trois points à droite. On a ainsi P3,3 = 6.
De façon générale, on peut écrire P3,n = P3,n‒1 + n, ce qui est une formule à la fois arithmétique et géométrique puisqu’elle signifie qu’on ajoute n éléments à droite du triangle précédent. On en déduit l’expression
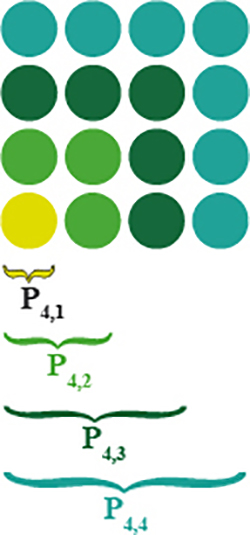
Pour les nombres carrés, notés P4,n, le principe est le même. On part d’un carré élémentaire à un point, puis on ajoute trois points autour pour former un carré, puis cinq, et ainsi de suite. De façon générale, on a : P4,n = n2.
Et ainsi de suite pour les polygones suivants (pentagone, hexagone…). Pour les nombres hexagonaux, on a et pour les nombres pentagonaux, on a P6,n = n(2n ‒ 1).


On peut aussi construire des nombres en trois dimensions, comme les nombres tétraédriques, les nombres cubiques et les nombres octaédriques, voire en dimensions 4 avec les nombres hypersolides ! Mais revenons au plan.
L’Euclide de l’arithmétique
La représentation figurée des nombres ne s’arrête pas au triangle : toutes les figures géométriques régulières sont utilisées pour filer la métaphore. Nicomaque de Gérase est le premier à proposer une table fournie et ordonnée des nombres figurés :
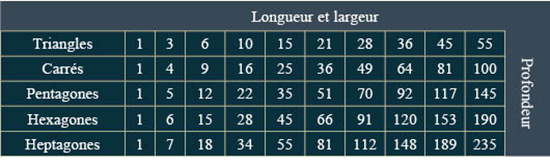
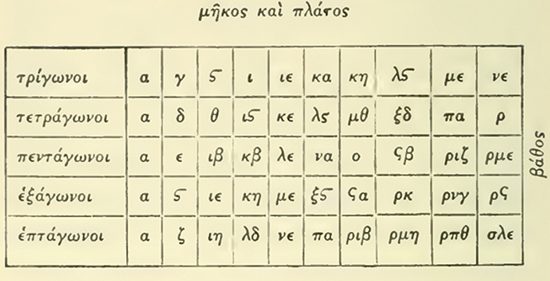
© Ivor Thomas, Greek Mathematical Works Thales to Euclid: Volume I, Loeb Classical Library, 1939, p. 98
Reproduction du tableau présenté par Nicomaque.
Nicomaque, que l’on surnomma l’Euclide de l’arithmétique, présente un résultat général sur la décomposition des nombres figurés (Introduction à l’arithmétique, II, 12, 5-6). Tout nombre carré est la somme du nombre triangulaire immédiatement au-dessus de lui dans le tableau et du nombre triangulaire immédiatement à gauche de ce dernier. Ainsi, 16 = 10 + 6, de même que 25 = 15 + 10.
De même, tout nombre pentagonal peut se décomposer en la somme du nombre carré immédiatement au-dessus de lui et du nombre triangulaire de rang directement inférieur. Ainsi, 12 = 9 + 3, tout comme 70 = 49 + 21.
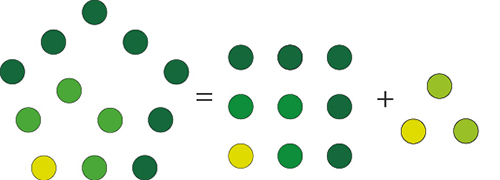
De façon plus générale, tout nombre p-gonal d’ordre n se décompose en la somme du nombre (p‒1)-gonal d’ordre n et du nombre triangulaire d’ordre n ‒ 1. Ce résultat est très important pour Nicomaque (et l’est tout autant dans le texte de Boèce) parce qu’il fait écho à une propriété géométrique : toute figure peut être décomposée en des triangles. Ainsi, grâce à ce résultat, Nicomaque entend montrer une forme d’harmonie entre la géométrie et l’arithmétique.
Le triangle, principe de la géométrie et del’arithmétique selon Boèce
« Toute figure triangulaire, carrée, pentagonale, hexagonale, ou toute figure quelconque limitée par plusieurs angles, si l’on mène des lignes à chaque angle depuis le milieu, est divisée en autant de triangles que la figure elle-même se trouve contenir d’angles : le carré, si l’on mène des lignes de cette façon, en quatre triangles; le pentagone, en cinq ; l’hexagone, en six ; et toutes les autres figures sont partagées en triangles selon la quantité des angles qui les mesurent, comme on le voit ci-dessous.
Carré divisé en quatre triangles :

Pentagone divisé en cinq triangles :

Hexagone divisé en six triangles :

Mais le triangle, si on le divise de cette manière, ne se résout pas en d’autres figures que lui-même. Il se ramène, en effet, à trois triangles.
Triangle divisé en trois triangles :
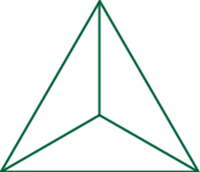
Il est si vrai que cette figure est la première figure de surface, que toutes les autres se résolvent en elle, tandis qu’elle-même, ne dépendant d’aucun autre principe et ne tirant son origine d’aucune autre figure de surface, se résout en elle-même. Eh bien, la même chose se produit avec les nombres. »
Boèce, Institution arithmétique, II, 6 (op. cit., p. 93-95).
D’autres nombres figurés
Passons en dimension 3. On peut imaginer des nombres pyramidaux à base triangulaire pour transposer les nombres triangulaires du plan. Pour les obtenir, il suffit d’ajouter deux nombres triangulaires consécutifs.
Triangles :

Pyramides à base triangulaire :

Nicomaque étudie ensuite les nombres pyramidaux à base carrée, les nombres cubiques et les nombres sphériques, comme dans une suite logique des figures régulières. Mais il s’intéresse aussi à des figures non régulières comme le rectangle. Il appelle alors figures hétéromèques les nombres dont un côté est plus long que l’autre d’une unité. Ce sont donc les nombres 2 = 1 × 2, 6 = 2 × 3, 12 = 3 × 4, 30 = 4 × 5, 30 = 5 × 6, 42 = 6 × 7… Il remarque alors une propriété qui lie les nombres triangulaires, carrés et hétéromèques.
Recensons dans un premier temps les premiers nombres carrés et hétéromèques.
Tétragones :

Hétéromèques :

Puis mélangeons-les en les alternant. Entre eux apparaissent les nombres triangulaires :

Toujours dans une perspective arithmologique, Nicomaque s’interroge sur le lien entre ces nombres figurés et les deux grandes familles des nombres : pairs et impairs.
La construction visuelle des nombres carrés permet de comprendre, à l’œil nu, que les nombres carrés sont engendrés par les impairs. En effet, si l’on prend le quatrième nombre, on voit qu’il est composé d’un jeton jaune (le premier nombre carré), puis de trois jetons vert clair (pour former le deuxième nombre carré), puis de cinq jetons vert foncé (complétant le troisième nombre carré) puis de sept jetons turquoise. Les nombres carrés s’organisent en partant de 1 (la diagonale) puis en y ajoutant des multiples de 2 (pour former les bords), ce qui signifie qu’on additionne des nombres impairs. Ainsi, on obtient ce très joli résultat :
12 = 1,
22 = 1 + 3,
32 = 1 + 3 + 5,
42 = 1 + 3 + 5 + 7…
n2 = somme des n premiers impairs.
Les carrés naissent donc dans les impairs. Mais que vont bien pouvoir engendrer les pairs ? Réponse : les hétéromèques ! En effet :
2 = 2,
6 = 2 + 4,
12 = 2 + 4 + 6,
20 = 2 + 4 + 6 + 8…
nième hétéromèque = somme des n premiers pairs.
Deux autres propriétés arithmétiques
Les nombres impairs ont la propriété d’engendrer non seulement les nombres carrés, mais aussi les nombres cubiques :
13 = 1,
23 = 3 + 5,
33 = 7 + 9 + 11,
43 = 13 + 15 + 17 + 19…
La combinaison des deux résultats concernant les impairs est restée connue sous le nom de théorème de Nicomaque : la somme des n premiers cubes est égale au carré de la somme des n premiers entiers. On peut le visualiser avec les nombres de la tetraktys :
13 + 23 + 33 + 43
= (1) + (3 + 5) + (7 + 9 + 11) + (13 + 15 + 17 + 19)
= la somme des dix premiers impairs
= 102
= (1 + 2 + 3 + 4)2.
La formule générale de Diophante
Si les pythagoriciens et néopythagoriciens se sont intéressés aux nombres figurés, ils ne furent pas les seuls. La Souda, une encyclopédie byzantine de la fin du Xe siècle, mentionne ainsi un traité sur le sujet de la main de Philippe d’Oponte, un disciple de Platon, dont on n’a malheureusement rien conservé. Diophante rend hommage à Hypsiclès (IIe siècle avant notre ère) pour sa définition des nombres figurés : à savoir, que l’on peut les considérer comme des sommes de suites arithmétiques.
C’est à Diophante (environ IIIe siècle) que l’on doit justement l’énoncé le plus puissant et le plus général sur le sujet : la formule permettant d’obtenir tous les nombres figurés. Ce résultat vient d’un petit traité de Diophante, le De polygonis numeris (tel qu’on le cite habituellement dans sa traduction latine). Il se trouve que la fin de ce traité est perdue : on n’en possède que les quatre premières propositions ; or, c’est dans la cinquième que devait se trouver la formule ! Heureusement, les premières propositions présentent déjà une relation qui permet de déduire la formule générale.
Dans un premier temps, Diophante montre que, ayant un nombre p-gonal F d’ordre n,
8F(p‒2) + (p‒4)2 est un nombre carré. Plus précisément, il montre que :
8F(p‒2) + (p‒4)2 = (2 + (p ‒ 2)(2n ‒ 1))2.
Ce résultat permet de déduire une formule générale donnant la valeur de tout nombre figuré en fonction de son nombre d’angles p et de son ordre n :
On ne peut pas assurer que cette expression était bien présente dans le traité de Diophante mais, puisqu’il possédait la première, qui est équivalente, on peut sans prendre trop de risque la lui attribuer !
références
• Les nombres. Bibliothèque Tangente 33, 2019. • Mathématiques et musique. Bibliothèque Tangente 11, 2022. • La gamme pythagoricienne. In Itération et récurrence, Bibliothèque Tangente 76, 2021. • Dossier « La saga des théorèmes : Pythagore ». Tangente 172, 2016.


