
Gauss et l’optique géométrique
Gauss est connu des mathématiciens comme… mathématicien. Mais nombre de ses recherches couvraient le champ de la physique. On lui doit des découvertes significatives en électricité (loi de Kirchhoff), en optique et en électromagnétisme (équations de Maxwell). Ses travaux en optique reposent sur ce qui est aujourd’hui identifié comme l’approximation de Gauss. En gros, il s’agit de considérer les lentilles sphériques comme des objets sans épaisseur, représentés comme des segments de droite dont on construit la médiatrice : l’axe optique. On se limite aux rayons « peu inclinés et peu éloignés » de cet axe. On suppose que les lentilles sont stigmatiques (l’image d’un point est un point) et aplanétiques (l’image d’un objet perpendiculaire à l’axe optique est perpendiculaire à l’axe optique). Alors pour construire l’image d’un point P il suffit de considérer deux rayons issus de P ; tous les autres issus de P passeront par le point image. Cette approximation en apparence grossière est en fait souvent applicable en pratique et simplifie grandement les relations mathématiques de l’optique géométrique.
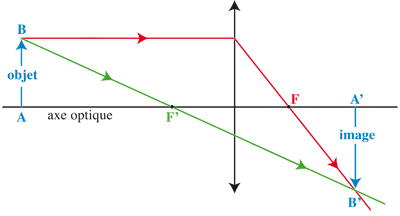
Choix du modèle, méthode de résolution…
Le réel est complexe… Pour le gérer, il faut synthétiser des ensembles d’observations cohérentes en lois, qui prennent souvent la ...
Lire la suite gratuitement
