
À chaque point (x, y) du plan, on associe naturellement une « altitude » z, fonction de x et de y, que l’on notera aussi f (x, y). La visualisation en trois dimensions des points de coordonnées (x, y, f (x, y)) produit quelque chose qui peut ressembler à une piste de ski.
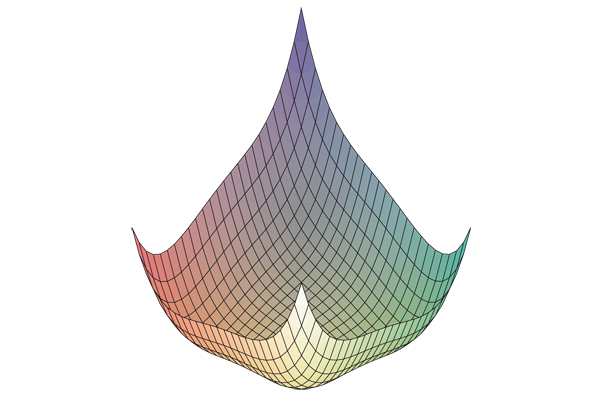
Graphe de la fonction qui au nombre x associe f ( x, y ) =x 4 + y 4 – 2( x – y ) 2.
Dans l’exemple du schéma, il est apparent qu’il y a un point quelque part qui se trouve plus bas que tous les autres. C’est celui-là que le skieur fatigué par une longue journée sportive voudrait trouver. Mathématiquement, il s’agit de déterminer les valeurs de x et de y pour lesquelles l’altitude, f (x, y), est minimale. Comment le localiser ?
L’art de l’approximation
Une idée consiste à partir d’un point quelconque (x, y) du plan, puis d’examiner les valeurs de f aux points qui l’entourent, à savoir les points de coordonnées (x + h, y + k), où les valeurs de h et de k sont supposées « suffisamment proches » de 0. Dans ces hypothèses, on dispose de l’approximation suivante :
