Le tirage de boules de couleur dans des urnes est un classique incontournable des ouvrages de probabilité. Habituellement, on se contente de remettre la dernière boule sortie dans l'urne avant de procéder à un nouveau tirage. Les modèles évoqués ici sont plus « dynamiques » dans la mesure où le contenu de l'urne ou des urnes va se modifier au cours du temps en fonction des tirages successifs.
Les urnes de Polya
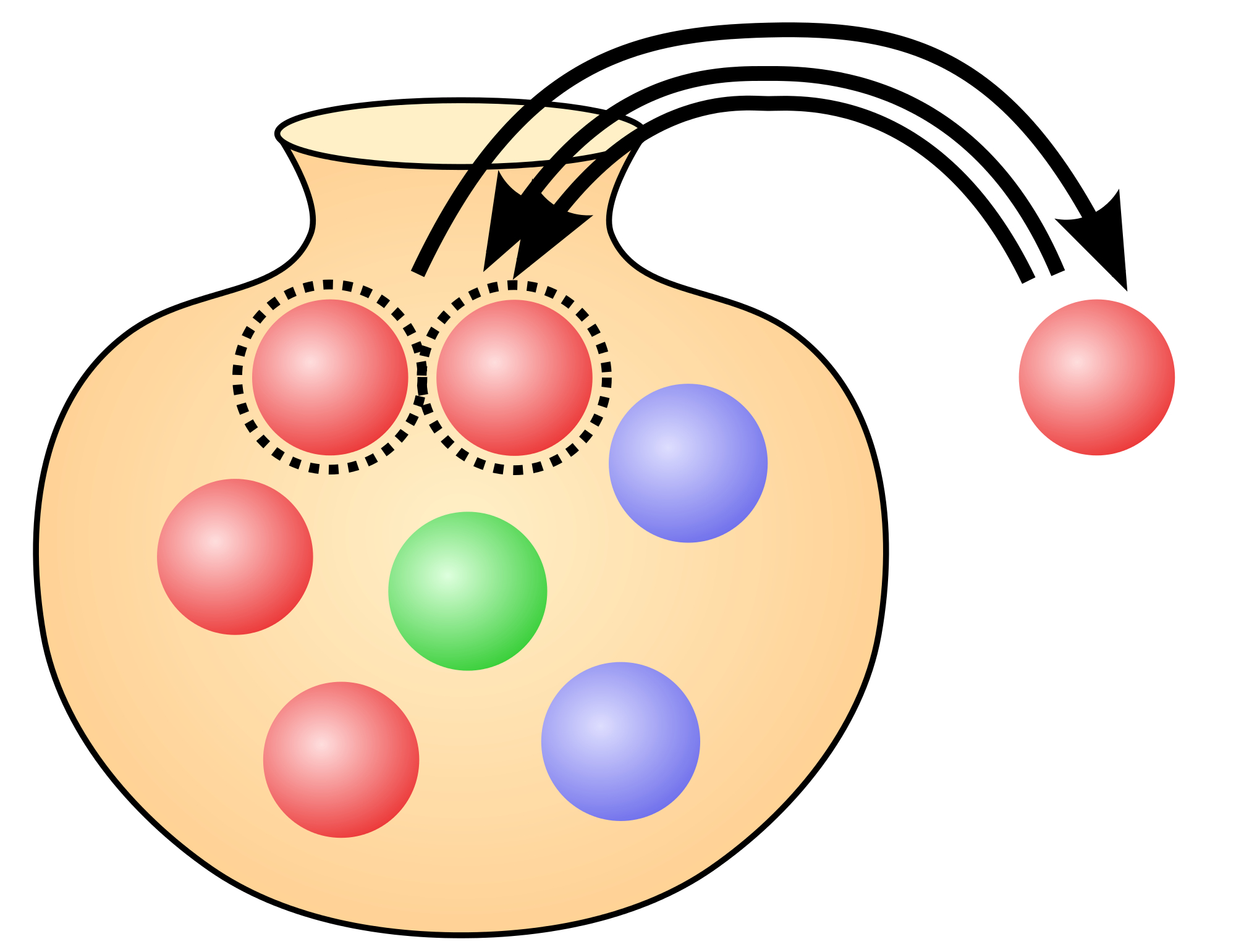
![]() Un premier modèle est celui des urnes de Polya, modèle imaginé par le grand mathématicien américano-hongrois George Polya (1887-1985). Dans ce modèle, on dispose d'une urne contenant a boules blanches et b boules noires. A chaque tirage, on tire une boule de l'urne, puis on la remet dans l'urne en ajoutant une autre boule de la même couleur que celle de la boule tirée. Le contenu de l'urne et le rapport du nombre de boules blanches sur le nombre total de boules vont donc varier et, si l'on procède à un grand nombre de tirages, le rapport blanches/total va tendre à se stabiliser vers une valeur limite.
Un premier modèle est celui des urnes de Polya, modèle imaginé par le grand mathématicien américano-hongrois George Polya (1887-1985). Dans ce modèle, on dispose d'une urne contenant a boules blanches et b boules noires. A chaque tirage, on tire une boule de l'urne, puis on la remet dans l'urne en ajoutant une autre boule de la même couleur que celle de la boule tirée. Le contenu de l'urne et le rapport du nombre de boules blanches sur le nombre total de boules vont donc varier et, si l'on procède à un grand nombre de tirages, le rapport blanches/total va tendre à se stabiliser vers une valeur limite.
 Ainsi, si l'on part d'une urne contenant une boule blanche et une boule noire, on obtient sur un grand nombre d'expériences des valeurs limites du rapport boules blanches / total des boules réparties de manière à peu près uniforme sur l'intervalle [0 ; 1], comme le montre cette image extraite du site internet http://www.suhasmathur.com/the-bayesian-observer qui retrace, avec des couleurs différentes, un certain nombre d'expériences de 200 tirages.
Ainsi, si l'on part d'une urne contenant une boule blanche et une boule noire, on obtient sur un grand nombre d'expériences des valeurs limites du rapport boules blanches / total des boules réparties de manière à peu près uniforme sur l'intervalle [0 ; 1], comme le montre cette image extraite du site internet http://www.suhasmathur.com/the-bayesian-observer qui retrace, avec des couleurs différentes, un certain nombre d'expériences de 200 tirages.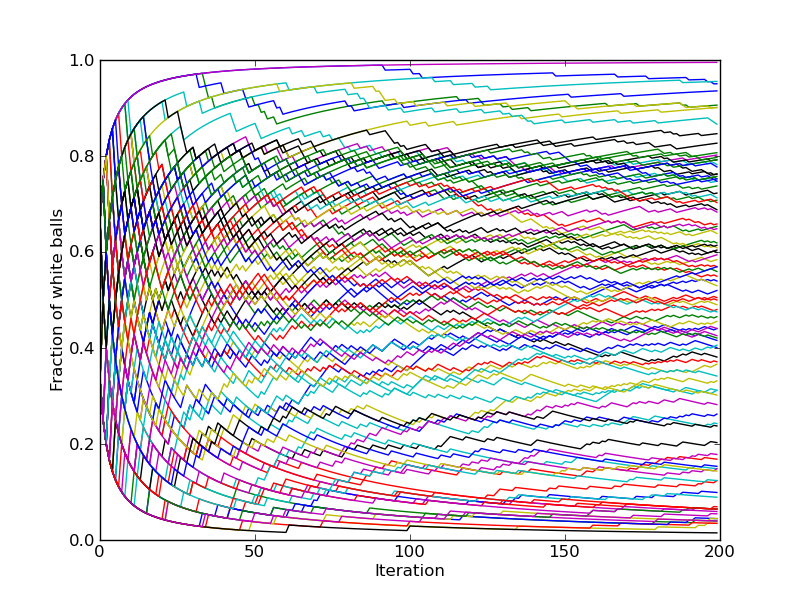
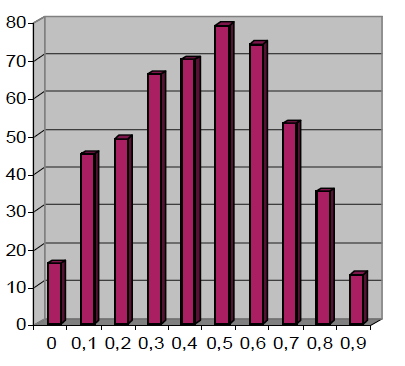
Curieusement, si l'on part de 2 boules blanches et 2 boules noires, la répartition des valeurs limites du rapport boules blanches / nombre total de boules n'est plus uniforme. On obtient alors une courbe du second degré de la forme f(x) = k x (1 – x).
Les urnes d'Ehrenfest
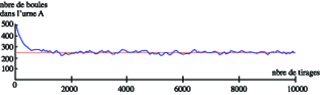
Un autre modèle d'urnes interagissantes est celui du physicien autrichien Paul Ehrenfest (1880 - 1933). Dans ce modèle, on dispose de deux urnes A et B et de N boules toutes de la même couleur mais numérotées de 1 à N. Au départ, toutes les boules sont dans l'urne A, l'urne B étant vide.
On tire ensuite aléatoirement un numéro n entre 1 et N et on transfère la boule portant le numéro n dans l'urne où elle n'était pas. Vers quelle situation le contenu des urnes va-t-il évoluer ?
L'exemple ci-dessous montre l'évolution pour 10 000 tirages avec un contenu initial de 500 boules dans l'urne A.