Le nombre de l'année est un nombre entier naturel non nul dont l'écriture décimale ne comporte qu'un seul chiffre répété, et qui est en outre divisible par le millésime de l'année en cours. Ainsi, en 2015, le premier nombre de l'année était le nombre
55 555 555 555 555 555 555 555 555 555, dont l'écriture comporte vingt-neuf chiffres 5. Le lecteur pourra vérifier qu'il n'en existe pas de plus petit !
1. L'année 2016 ne possédait aucun nombre de l'année. Vous saurez certainement le démontrer…
Qu'en sera-t-il de 2017 ? L'année 2017 possédera bien des nombres de l'année. Le plus petit d'entre eux comportera deux mille seize chiffres 1. Les lecteurs courageux effectueront la division…

Les Anglo-Saxons appellent ces nombres qui ne s'écrivent qu'avec des chiffres 1 des repunits (pour « unité répétée »).
Quelle sont les années qui possèdent des nombres de l'année et quelles sont celles qui n'en possèdent pas ? Déjà, toutes les années dont le millésime est un nombre premier impair (comme 2017) possèdent bien des nombres de l'année. Cette propriété découle directement du petit théorème de Fermat. En effet, si p est un nombre premier et a un entier premier avec p, alors a p–1 – 1 est divisible par p.
Le nombre 2017 est un nombre premier, et 10 est premier avec 2017. On en déduit que 102 016 – 1 est divisible par 2 017. Le nombre 102 016 – 1 est un nombre qui s'écrit, en base 10, avec deux mille seize chiffres 9. Il est évident que le nombre (102 016 – 1) / 9, notre repunit vu ci-dessus, est aussi divisible par 2 017.
Il se trouve que, pour 2 017, ce nombre est le plus petit nombre de l'année. Mais le plus petit nombre de l'année d'un millésime premier impair p comporte-t-il obligatoirement p – 1 chiffres ?
Absolument pas ! Cependant, son nombre de chiffres doit être un diviseur de p – 1. Ainsi, prenons une année du début de notre ère, comme l'an 13. Le plus petit nombre de cette année ne comportait pas douze chiffres 1, mais seulement six (qui est bien un diviseur de 12). Le lecteur vérifiera que 111 111 est divisible par 13 et que c'est le plus petit.
Et une bonne année…
Si l'on veut revenir à notre époque, prenons l'exemple de 2027, qui sera la prochaine année première après 2017. Le plus petit nombre de l'année 2027 s'écrira avec « seulement » mille treize chiffres 1.
Pour les années dont le millésime est un nombre composé dont la décomposition ne comporte que des facteurs premiers distincts (sans facteurs carrés) autres que 2 et 5, le plus petit nombre de l'année aura un nombre de chiffres égal au plus petit commun multiple des nombres de chiffres des nombres de l'année de chacun des facteurs premiers. Lorsque les facteurs premiers seront présents avec un exposant supérieur ou égal à 2, la détermination du nombre de chiffres du plus petit nombre de l'année sera un peu plus compliquée.
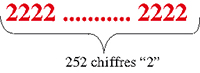
Qu'en est-il pour les années dont le millésime comporte des facteurs 2 ou 5 ? Prenons l'exemple du millésime de l'année 2018, qui est le double d'un nombre premier. Le plus petit nombre de l'année 2018 s'écrira avec deux cent cinquante-deux chiffres 2 (252 est bien un diviseur de 1 009 – 1).
De même, le plus petit nombre de l'année 4036 s'écrira avec deux cent cinquante-deux chiffres 4, celui de l'année 8072 avec deux cent cinquante-deux chiffres 8, mais les multiples de 1 009 par une puissance de 2 d'exposant strictement supérieur à 3 n'auront pas de nombre de l'année. Mais 2015 possède des nombres de l'année.
2. Quels sont les millésimes multiples de 5 qui possèdent des nombres de l'année et ceux qui n'en possèdent pas ?

