Le jeu de Hackenbush se pratique sur un ensemble de graphes posés sur un « sol » représenté en pointillés. La règle est simple. Les joueurs, à tour de rôle, effacent un arc de leur choix ; toute portion de graphe qui n’est alors plus reliée au sol après cet effacement est également ôtée. Lorsqu’un joueur ne peut plus jouer, il perd la partie.
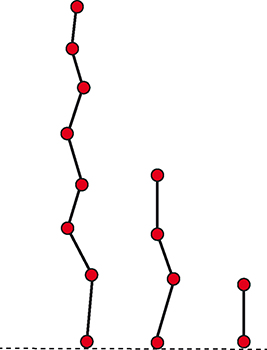
Si les graphes ne sont constitués que de simples tiges sans embranchement (comparables à des tiges de bambous), le jeu est parfaitement analogue au jeu de Nim à plusieurs tas. La stratégie pour ce jeu est de calculer la somme-Nim de l’ensemble qu’on laisse à son adversaire. Si on lui laisse une situation dont la somme-Nim vaut 0, il est dans une situation perdante et ne peut atteindre une situation gagnante, quel que soit le coup qu’il jouera ; au contraire, si on lui laisse une situation dont la somme-Nim est différente de 0, il gagnera à coup sûr s’il ne commet pas d’erreur.
Pour calculer la somme-Nim d’une situation, on écrit en base 2 les nombres d’arcs des différentes tiges et on additionne ces nombres sans prendre en compte les retenues. Par exemple, dans la figure précédente, les nombres de tiges sont respectivement égaux à 7, 3 et 1 (soit 111 + 11 + 1 calculé en base 2, sans les retenues, qui donne 101). On calcule que leur somme-Nim est égale à 5. Pour la ramener à 0, il faut supprimer le troisième arc de la plus longue tige, ce qui laisse la situation perdante 2–3–1 à l’adversaire.
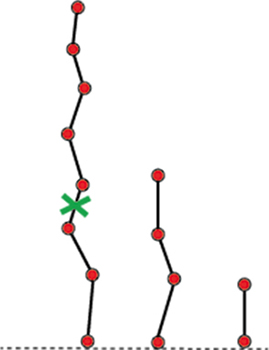
Si les trois tiges étaient réunies en « touffe », les trois nœuds au sol étant confondus, le calcul se ferait de la même façon et le coup gagnant serait le même.
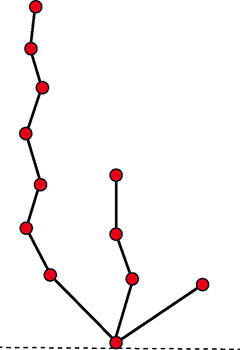
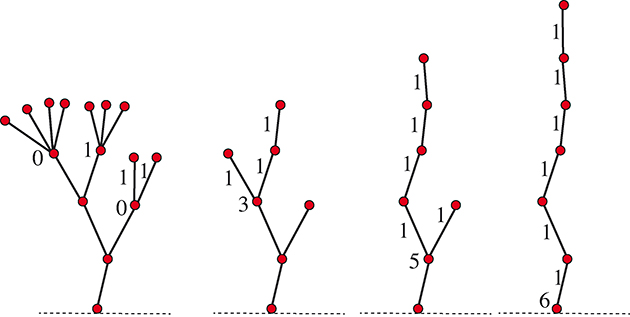
Voyons maintenant le cas d’un arbre. La solution est évidente dans le cas où il n’y a qu’un seul arbre : on efface l’arc partant du sol et on gagne. Mais on peut ramener un arbre à une seule tige en calculant la somme-Nim à chaque nœud.
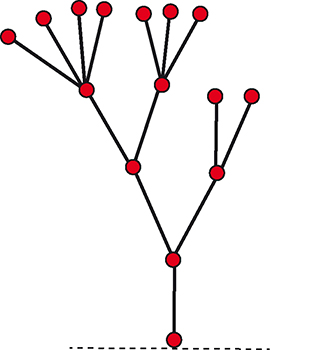
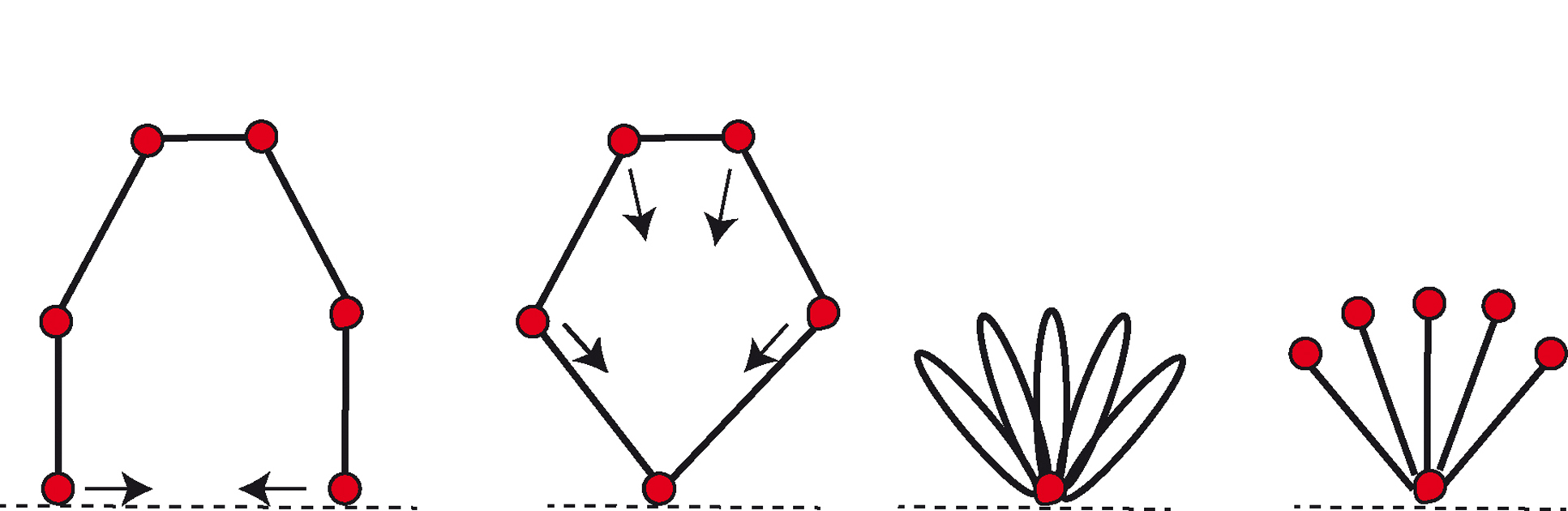
Une situation initiale de Hackenbush peut également présenter des circuits. Un circuit se « résout » en réunissant tous les noeuds de son pourtour, ce qui a pour effet de transformer les arcs en boucles, puis en remplaçant les boucles par des arcs simples.
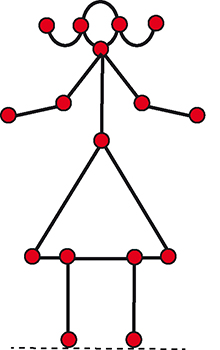
Si la situation initiale est la « jeune fille » représentée sur la figure, quel est le coup à jouer pour le joueur qui a le trait ?
John Conway a également proposé des variantes : le blue-red-Hackenbush, dans lequel chaque arc est colorié soit en bleu, soit en rouge, et où chaque joueur ne peut effacer que les arcs de sa couleur, et le green-blue-red-Hackenbush, dans lequel il existe en plus des arcs verts qui peuvent être effacés indifféremment par l’un ou l’autre joueur.