« Nous allons donc procéder à la diagonalisation de cette matrice afin de… »
Un vrombissement sourd interrompt une nouvelle fois le professeur Phi pendant le cours de mathémagie. Par les fenêtres de la classe, on peut voir une colonie de pelleteuses se mettre en branle dans un concert motorisé que l’épaisseur des vitres ne parvient qu’avec peine à atténuer.
« Par la barbe de Pythagore ! grommelle le professeur. Comment peut-on travailler dans ces conditions ?
– Nous serons contents d’avoir accès au métro une fois que sa construction sera achevée, ose Alpha. Nous pourrons atteindre n’importe quel point de la planète Prépaterra en quelques minutes !
– Moui, concède le professeur. Mais s’il y a une chose qui m’insupporte davantage que ce vacarme, ce sont bien les plans de ce chantier, qui ont été conçus de manière absolument non optimale. »
Dans la bouche du professeur Phi, il s’agit, ni plus, ni moins, que d’une offense suprême.
« D’ailleurs, poursuit-il avec une soudaine lueur dans le regard, il serait intéressant de voir si vous feriez mieux que les ingénieurs du projet “Tromé du Turfu”. »
Quelques pressions sur son communicateur remplacent, sur l’écran de la classe, le cours sur les endomorphismes par un tableau de chiffres.
« Voici les coûts estimés en millions de brouzoufs (MB) pour relier les différentes stations (qui, comme vous le savez, ont été nommées d’après d’illustres contributeurs au vénérable magazine Tangente, qui en est aujourd’hui à son vingtième siècle d’existence). »
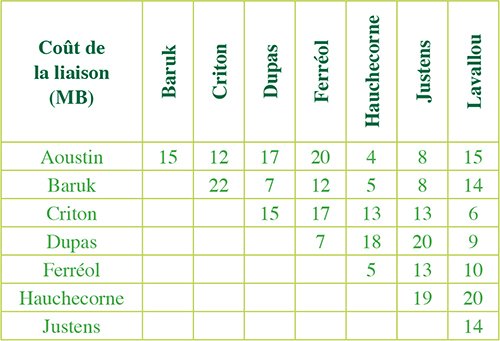
« À partir de ces données, vous devriez pouvoir trouver les connexions à réaliser pour minimiser le coût du métro, en faisant en sorte qu’il existe au moins un parcours pour se rendre d’une station à n’importe quelle autre. »
Et vous, cher lecteur, quelle méthode adopteriez-vous pour savoir quelles stations relier à moindre coût ?
Une contrainte due à l’Institut
Une fois le tracé optimal dessiné sur le tableau, la jeune Epsilon élève la voix. « Professeur Phi, je crois que nous avons oublié de prendre en compte une contrainte… Chacune des stations doit se trouver à dix minutes au plus de Hauchecorne, qui est la station permettant d’accéder à l’Institut intergalactique. Cela doit avoir un impact sur le tracé final…
– Effectivement, concède Phi. »
Il affiche un nouveau tableau, qui indique cette fois la durée en minutes des différentes connexions.
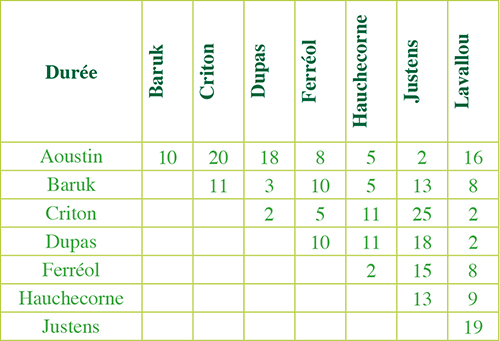
Cher lecteur, comment modifieriez-vous le tracé précédent pour faire respecter la contrainte mentionnée par Epsilon ?

