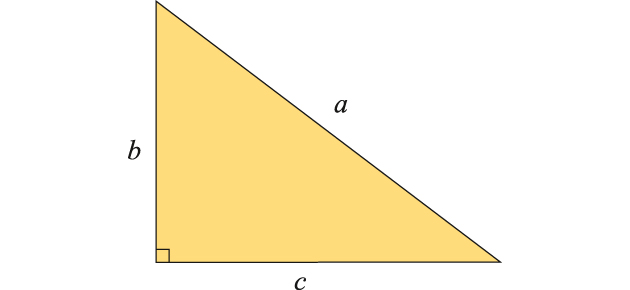
Dans un triangle rectangle, le carré de l'hypoténuse est égal à la somme des carrés des côtés de l'angle droit. Quand cette relation est vérifiée par trois nombres entiers, on parle de triplets pythagoriciens. Qui sont ces nombres, comment les caractériser ?

D'après le théorème de Pythagore, si a est l'hypoténuse d'un triangle rectangle, b et c les côtés de l'angle droit, a² = b² + c². On parle de triplets pythagoriciens si ces trois nombres sont des entiers pour une certaine unité de mesure. Dans ce cas, le triangle est rationnel dans le sens que les rapports de ses côtés sont des nombres rationnels. Réciproquement, un triplet pythagoricien correspond à un triangle rectangle rationnel.

Fermat : une remarque visionnaire

Le plus célèbre des triplets pythagoriciens, (3, 4, 5), correspond à la corde à treize nœuds utilisée par les bâtisseurs du Moyen Âge pour tracer des angles droits.

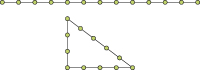
^{La corde à treize nœuds.}

Ces triplets peuvent être entièrement décrits en suivant la démarche que Diophante utilise pour résoudre le problème qu'il pose dans le livre II de son Arithmétique : « Partager un carré proposé en deux carrés. »
Les solutions de cette énigme constituent les triplets pythagoriciens, qui se trouvent également chez Euclide, mais sous forme géométrique. L'originalité de Diophante est de poser et de ... Lire la suite

Les quadruplets pythagoriciens

La notion de triplet pythagoricien se généralise aux quadruplets, en remplaçant un triangle par un parallélépipède. On obtient la formule suivante : a² + b² + c² = d², avec a la largeur, b la longueur, c la hauteur et d la longueur de la grande diagonale du parallélépipède.

À partir de

$p'=\frac{1}{\sqrt{2}}, \, q'=\frac{2}{\sqrt{2}}, \, r'=\frac{3}{\sqrt{2}},$

on obtient $2^2+3^2+6^2=7^2$

Tout comme pour les triplets, il est possible de caractériser les quadruplets pythagoriciens : si a = m(p² + q² – r²), b = 2mpr, c = 2mqr et d = m(p² + q² + r²), avec m, p, q et r des entiers tels que p² + q² – r² > 0, alors (a, b, c, d) constitue un quadruplet pythagoricien. Pour les obtenir tous, il suffit de considérer les valeurs de a, b, c, d ainsi obtenues à partir de

$p'=\frac{1p}{\sqrt{n}}, \, q'=\frac{q}{\sqrt{n}}, \, r'=\frac{r}{\sqrt{n}},$

avec n un entier non nul. Des arguments élémentaires permettent alors d'obtenir une caractérisation systématique des quadruplets pythagoriciens.

Patrick Breen

Les triplets pythagoriciens

Hervé Lehning

dossier : La saga des théorèmes : Pythagore

Tangente 172 : Le théorème de Pythagore

Fermat : une remarque visionnaire