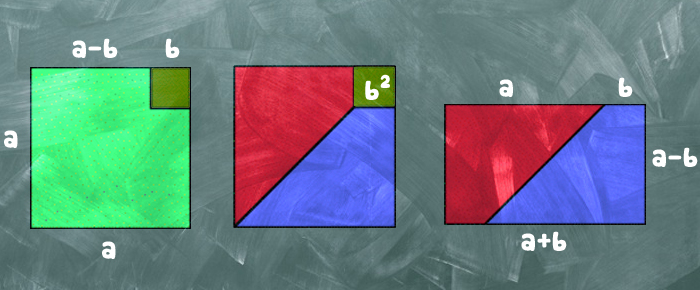
Les fameuses « identités remarquables » ont été, selon une longue tradition d'enseignement des mathématiques en France, l'un des piliers du calcul algébrique. Elles font partie – pas toujours explicitement d'ailleurs des savoirs transmis, enseignés et utilisés depuis qu'il existe des écoles mathématiques, mais si elles ont fait les beaux jours des programmes d'enseignement de l'algèbre au niveau du collège, elles n'apparaissent plus qu'en pointillés dans la version 2016 des programmes de troisième…
Toute une histoire…
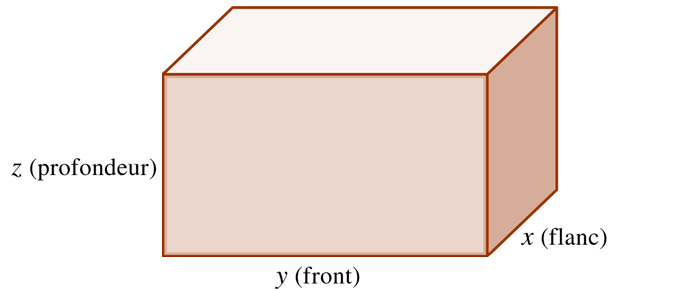
Environ deux mille ans avant notre ère, les Babyloniens de l'Ancien Âge consignaient déjà sur leurs tablettes destinées à l'enseignement des scribes « porteurs de savoir » des problèmes avec solutions où intervenaient largement les identités remarquables. Ils recherchaient par exemple deux nombres connaissant leur somme et leur produit, dans un étonnant problème concret : « Une cave. Le flanc, le front [inverses l'un de l'autre], la profondeur, somme du flanc et du front. J'ai extrait 26 de terre. Que sont le flanc ? le front ? la profondeur ? » Nous dirions aujourd'hui : rechercher x (le flanc), y (le front), z (la profondeur) d'une cave sachant que xy = 1, x + y = z et xyz = 26.