
« “Voyez-moi ça ! dit le diable.[…] Continuons à assembler les cubes. La pierre suivante vient toujours se placer sur la jointure entre les deux qui sont en-dessous, comme font les maçons.” […] Et ils continuèrent jusqu'à ce que le triangle soit terminé. […] Le démon des maths grimpa le long d'un des côtés du triangle et écrivit un “1” sur le cube situé au sommet. […] “Sur chaque cube, nous écrivons toujours le résultat de l'addition des nombres placés au-dessus.
– Un jeu d'enfant”, dit Pierre. »
Comme Pierre, l'enfant en proie au « démon des maths » dans ses rêves, admirablement contés par Hans Magnus Enzensberger dans le titre éponyme (Le Seuil/Métaillé, 1998), nous irons de découverte en découverte au cœur du triangle de Pascal.
D'innombrables figures numériques
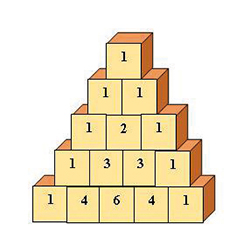
Le triangle suggéré par le démon des maths.
« “Ce triangle contient encore bien mieux” affirme le démon des maths à Pierre, déjà émerveillé par cet entassement triangulaire de cubes ne possédant pour propriété que celle de son algorithme de construction. Blaise Pascal avait, déjà, dans l'étude détaillée qu'il a faite de “son” triangle en 1653, décelé une multitude de propriétés découlant de cet empilement, révélant : “J'en laisse bien plus que je n'en donne. C'est une chose étrange ... Lire la suite
