
Pourquoi moins par moins fait-il plus ? Pour résoudre ce premier mystère, transportons-nous dans un monde plus graphique, celui de la droite orientée des réels (« orienter » signifie, étymologiquement, « tourner vers l'Orient », donc vers la droite sur la rose des vents).
On choisit une origine O. À chaque nombre réel m, on peut associer un point M tel que la valeur algébrique soit égale à m. On peut même associer à m le vecteur
.
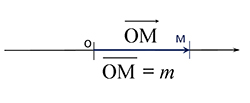
Association du point M au nombre réel m
Transformer les multiplications en rotations
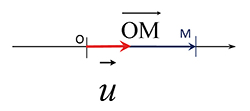
Grâce à cette représentation géométrique, les nombres « réels » prennent consistance. On peut alors se demander ce que signifie, dans ce cadre, de multiplier par 1, l'élément neutre de la multiplication : m × 1 = m. L'opération n'a pas d'effet visible, et revient à faire une rotation d'un angle 0° autour de l'origine.
Multiplier m par –1 consiste à passer de M à M', ce dernier point étant le symétrique de M par rapport à l'origine. C'est donc réaliser une rotation de 180°.
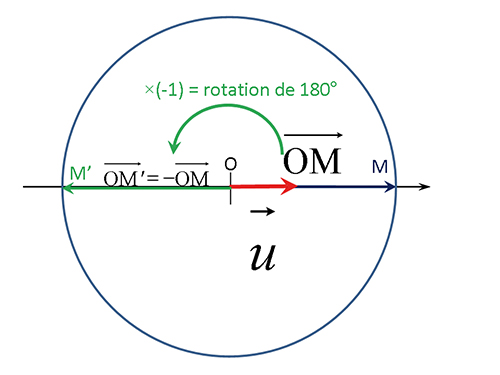
Construction de M', symétrique de M par rapport à O.
Avoir remplacé les multiplications par 1 ou –1 par des rotations permet d'expliquer ... Lire la suite
