
Inventés dès le milieu du xvie siècle avant tout pour résoudre des équations, les nombres complexes n'ont acquis un statut mathématique qu'au xviiie siècle, lorsque leurs propriétés algébriques ont été traduites géométriquement. Leur usage de « facilitateurs » de problèmes géométriques pouvait alors débuter…
Une histoire de nombres et de points
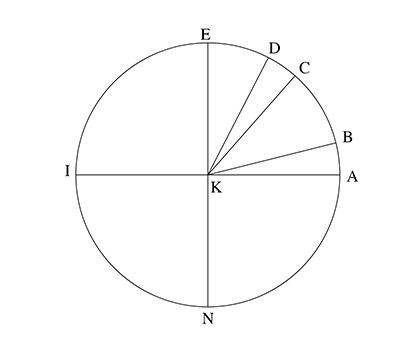
Représentation et multiplication des complexes selon Argand.
Lorsqu'en 1797 le Norvégien Caspar Wessel (1745–1818), arpenteur de son état, qui voyait sans doute dans les nombres complexes une manière de résoudre les triangles de son métier, présenta à l'Académie royale du Danemark son mémoire Essai de représentation analytique de la direction, il fut accepté car jugé d'un très bon niveau… mais resta dans l'oubli jusqu'à ce qu'un antiquaire le retrouve, en 1895 (!), où il fut enfin reconnu puis publié par Sophus Lie. L'approche de Wessel, qui utilise l'addition des « lignes possédant une longueur et une direction », nos actuels vecteurs, définit leur multiplication en ajoutant leurs angles polaires et en multipliant leur longueur.
En réalité, Wessel était un précurseur, car le Suisse Jean-Robert Argand (1768–1822), qui n'était pas non plus un mathématicien professionnel puisque comptable et libraire à Paris, publie en 1806, dans un petit livre cette fois, mais édité à compte d'auteur, ... Lire la suite
