
Le propre des logarithmes est de transformer les multiplications en additions, opérations bien plus aisées à effectuer. Par là même, ils transforment les divisions en soustractions et les exponentiations en multiplications. Or, une exponentielle réalise le contraire. Pour définir un logarithme, une idée simple consiste donc à inverser une exponentielle. Voyons la méthode avec celle de base 10. Par définition, log x est le nombre y tel que x = 10y.
Ainsi, log 1 = 0, log 10 = 1, log 100 = 2, etc. Voici un petit extrait d'une table de logarithme de base 10 :
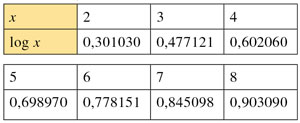
On peut y vérifier que log 4 = 2 log 2 et log 6 = log 2 + log 3. De façon générale, pour calculer le produit de deux nombres, disons 12,132 et 5,456, on cherche leurs logarithmes dans la table, ce qui donne ici log(12,132) = 1,083932402 et log(5,456) = 0,7368743616. On additionne ensuite ces deux nombres, ce qui donne le logarithme du produit P : log P = 1,820806764. En lisant la table à l'envers, nous obtenons alors P comme l'exponentielle de base 10 de ce dernier nombre, d'où P = 66,19219211, ce qui donne le résultat exact du calcul demandé en tronquant les deux ... Lire la suite
