
Les nombres premiers nous intriguent et nous fascinent depuis l'Antiquité, peut-être parce qu'ils sont en nous, si l'on en croit l'expérience que Karen Wynn a conduite en 1992 sur des bébés de 5 à 7 mois. Dès la petite enfance, le concept de nombre semble ancré dans le cerveau de l'être humain.

Un objet, puis un second
sont placés derrière
un obstacle qui, une fois ôté,
laisse bien apparaître deux objets.
Le bébé s'attend à ce résultat :
son attention ne reste pas
focalisée longtemps.
Cette expérience est similaire
à la précédente, sauf qu'avant
d'ôter l'obstacle l'expérimentatrice
subtilise discrètement
l'un des deux objets ;
il n'en reste donc plus qu'un.
L'attention du bébé reste alors fixée
durant plusieurs dizaines de secondes.
Parmi les entiers naturels se trouvent les nombres premiers, ceux, comme 2, 3, 5, 7 ou encore 2017, qui ne sont divisibles par aucun autre. Godfrey Hardy s'adressait ainsi, en 1922, à ses collègues physiciens :
« C'est le mathématicien qui a le contact le plus direct avec la réalité. […] 317 est un nombre premier non parce que nous le pensons ou parce que notre esprit est constitué d'une certaine manière, mais parce que c'est ainsi, parce que la réalité mathématique est ainsi faite. »
Les premiers résultats sur les nombres premiers sont dus à Euclide (vers –300) : tout entier est représentable comme produit de nombres premiers. On peut ainsi voir les nombres premiers comme les briques élémentaires dont tous les autres entiers sont constitués. En outre, la décomposition d'un entier en ses facteurs premiers est unique ; c'est d'ailleurs la raison pour laquelle, par convention et par commodité, on exclut 1 de la liste des nombres premiers. Enfin, Euclide démontre qu'il existe une infinité de nombres premiers.
Compter, une activité humaine
L'étude de la suite des nombres premiers a passionné Paul Erd?s tout au long de sa vie. Né sur les bords du Danube, à Budapest, le 26 mars 1913, au moment où ses deux grandes sœurs, Magda et Clara, décèdent des suites de la scarlatine, Erd?s sera essentiellement éduqué à la maison par sa mère, Anna, professeure de mathématiques. Il entretiendra avec elle, durant toute sa vie, une relation fusionnelle.
Sa production scientifique sera exceptionnelle, avec plus de mille cinq cents articles, et plus de cinq cents collaborateurs, en théorie des nombres, analyse combinatoire, théorie des graphes, géométrie des nombres, probabilités, analyse mathématique, théorie des ensembles. Erd?s était non seulement curieux de tout mais aussi extrêmement généreux pour partager ses idées ; les mathématiques étaient à ses yeux un bien commun.
Erd?s avait un don spécifique, celui de cristalliser toute la difficulté d'un problème général dans une formulation particulière. On découvre aujourd'hui encore, avec stupéfaction, que ses résultats, tout comme les méthodes qu'il a mises en place, même sur des problèmes très spécifiques en apparence, sont en fait extrêmement profonds et féconds. Il décède en 1996 seul dans une chambre d'hôtel, ultime paradoxe pour celui qui toujours était entouré de collègues mathématiciens.
À 18 ans, Erd?s commence ses recherches sous la direction de Leopold Fejér (1880–1959). Il s'intéresse au problème suivant (le fameux postulat de Bertrand), posé par Joseph Bertrand au milieu du XIXe siècle : existe-t-il toujours un nombre premier entre un entier n et son double 2n ? En 1850, Pafnouti Tchebychev a pu confirmer cette hypothèse, à l'aide d'une preuve techniquement difficile. En 1931, Erd?s donne une démonstration plus simple et directe. Ce fut le premier coup d'éclat de ce tout jeune mathématicien.
L'une des grandes questions de la théorie des nombres est la suivante : combien existe-t-il de nombres premiers inférieurs à un nombre x > 0 donné ? On note p(x) ce nombre. Aucune formule exacte (et utilisable) n'ayant pu être exhibée, on a essayé plus modestement d'approcher p(x).
Sur la base d'observations heuristiques, Adrien-Marie Legendre (1752–1833) et Carl Friedrich Gauss (1777–1855) avaient conjecturé que p(x) est « proche » de x / ln(x), où ln désigne le logarithme népérien (voir notre dossier sur les logarithmes dans ce numéro). On en déduit une loi de raréfaction quantitative, des nombres premiers.
En 1896, la conjecture est enfin démontrée, indépendamment, par Jacques Hadamard (1865-1963) et Charles-Jean de La Vallée-Poussin (1866-1962). Les deux preuves proposées font cependant appel à l'analyse complexe. Une question importante émerge alors : peut-on trouver une démonstration « élémentaire » de ce résultat, en ce sens qu'elle resterait cantonnée à l'analyse réelle, sans jamais faire appel aux nombres complexes ?
En 1949, Paul Erd?s et Atle Selberg produisent une telle démonstration, réglant ainsi les statuts respectifs de l'analyse complexe et de l'analyse réelle : si l'on peut encore dire, avec Hadamard, que « le chemin le plus court entre deux quantités réelles passe nécessairement par le plan complexe », on ne peut pour autant établir de hiérarchie entre les deux théories.
L'émergence des probabilités
En 1934, le jeune Erd?s quitte la Hongrie pour se rendre à Cambridge. Il y rencontre Hardy et discute avec lui des résultats que ce dernier a obtenus en 1917 avec le prodige indien Srinivasa Ramanujan (1887-1920). Hardy et Ramanujan se sont intéressés à la factorisation d'un entier « pris au hasard ». Combien cet entier possède-t-il de facteurs premiers ? On s'attend à ce qu'un nombre « pris au hasard » soit divisible par 2 une fois sur deux, divisible par 3 une fois sur trois, divisible par 5 une fois sur cinq… On qualifiera de normal un tel entier. En particulier, un nombre normal n'est ni un carré, ni un nombre premier.
En 1917, Hardy et Ramanujan publient un article qui peut être considéré comme l'acte de naissance de la théorie probabiliste des nombres. On y trouve le résultat suivant : en moyenne, un entier possède ln(ln n) facteurs premiers. En outre, cette valeur moyenne est également la valeur normale. Autrement dit, le nombre de facteurs premiers d'un entier « pris au hasard » ne dépend, statistiquement, que de sa taille (son ordre de grandeur). C'est tout à fait spectaculaire, et pour le moins contre-intuitif !
Cinq années après sa rencontre avec Hardy, en 1939, Erd?s se trouve aux États-Unis, à Princeton (New Jersey). Il y rencontre Marc Kac (1914-1984), un mathématicien d'origine polonaise persuadé que le résultat de Hardy et Ramanujan cache en fait une loi gaussienne : la répartition des facteurs premiers d'un entier « pris au hasard » doit suivre, selon lui, une courbe de Gauss (voir Tangente 149). Quelques mois plus tard, Erd?s et Kac démontrent ce résultat. Plus précisément, si F(n) désigne le nombre de facteurs premiers de n et si l'on note F la fonction de répartition gaussienne, définie par
alors la probabilité que F(n) soit inférieur à s'approche de F(t) à mesure que n croît. Erd?s et Kac ont mis en évidence un modèle de la courbe de Gauss à partir des seuls nombres entiers ! Les entiers naturels présentent ainsi des comportements qui peuvent être naturellement décrits par des lois probabilistes classiques introduites dans des contextes étrangers à la théorie des nombres…
On peut dès lors se demander quels sont les phénomènes probabilistes modélisables à partir de la seule structure multiplicative des nombres entiers. Le mouvement brownien, que l'on peut décrire en première approximation comme le mouvement, dans un fluide, d'une particule qui ne serait soumise qu'aux chocs avec les petites molécules de ce fluide, est un objet probabiliste fondamental. Il relève lui aussi d'une modélisation reposant sur la répartition des diviseurs des entiers.
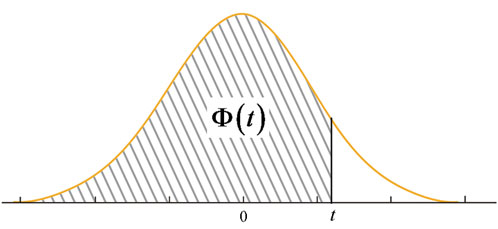
La quantité
 )
mesure l'aire
sous la fameuse
courbe en cloche.
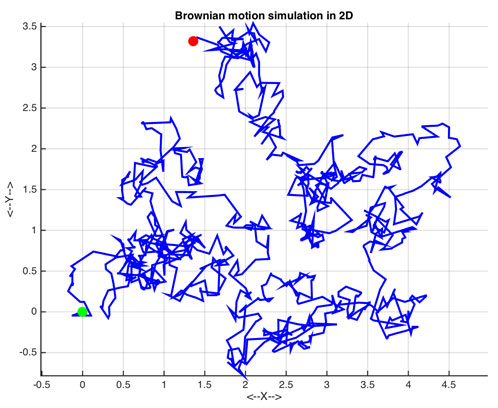
Simulation
d'un mouvement
brownien.
Des idées d'une grande actualité
En 1946, Erd?s produit un autre résultat sidérant, toujours en s'intéressant à la décomposition en facteurs premiers d'un entier n normal. En écrivant n = p1 p2 … pk, où p1 ≤ p2 ≤… ≤ pk désignent les facteurs premiers, alors ln(ln pj )est « proche » de j (pour 1 ≤ j ≤ k). C'est presque incroyable : pourquoi le douzième facteur premier d'un entier normal n serait-il « proche » de ln (ln 12) ? Il apparaît ainsi que la structure multiplicative intime de n ne dépend statistiquement que de sa taille !
Les idées probabilistes issues des résultats de Hardy-Ramanujan et d'Erd?s-Kac ont irrigué toute la recherche dans le domaine de la théorie probabiliste des nombres jusqu'à aujourd'hui. La fameuse conjecture (toujours ouverte) des nombres premiers jumeaux, selon laquelle il existe une infinité de nombres premiers p tels que p + 2 soit également un nombre premier, a elle-même été ébranlée récemment. En 2013, dans un article virtuose, Yitang Zhang a montré (voir Tangente 153) qu'il existe une infinité de couples de nombres premiers (p, q) tels que la différence | p – q | soit inférieure à 70 000 000. Quelques mois plus tard, James Maynard et (indépendamment) Terence Tao ont simplifié la démonstration. Le projet collaboratif Polymath8 a ensuite permis de réduire la borne 70 000 000 à 246… qui est cependant encore loin de la valeur 2 conjecturée – dont on a des raisons de penser qu'elle restera inaccessible tant que d'autres idées nouvelles n'auront pas été introduites.

