1 – Quatre nombres à placer
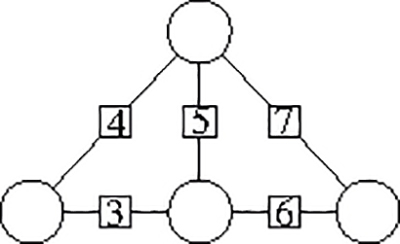
Placez les nombres 1, 2, 3 et 4 dans les disques de telle sorte que chaque nombre écrit dans un petit carré soit égal au total des deux nombres auxquels il est relié par un trait.
2 – Les carrés
Le jeune Mathis affirme : « Il y a dix-huit carrés dans cette figure. » Sa sœur Mathilde réplique : « Oui, si tu ne comptes que les petits carrés… mais il y a aussi des carrés moyens et des grands carrés ! »
Au total, combien la figure compte-t-elle de carrés entièrement dessinés ?
3 – À la maternelle
La maîtresse a distribué à chaque enfant d'un groupe une feuille avec ces trois symboles et trois feutres de trois couleurs différentes (un bleu, un rouge et un jaune). Elle leur donne la consigne de colorier l'intérieur de chaque symbole avec une couleur de façon que deux symboles d'une même feuille ne soient jamais de la même couleur.
Les enfants se sont appliqués et ont respecté la consigne. Seuls deux enfants du groupe ont des dessins identiques, les autres étant tous différents.
Combien le groupe compte-t-il d'enfants, au maximum ?
4 – La coccinelle
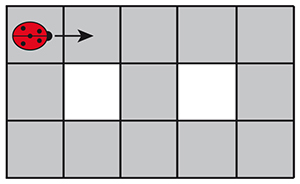
Une coccinelle se déplace sur les treize cases grisées d'un circuit. Le premier déplacement se fait dans le sens de la flèche. Elle se déplace d'une case par seconde et quand elle a le choix, elle peut aller d'un côté ou de l'autre, mais elle ne revient jamais en arrière.
Marquez d'une croix toutes les cases sur lesquelles elle peut se trouver après exactement onze secondes.
5 – L'anniversaire
« Avant-hier je n'avais encore que 8 ans, mais à la fin de l'année, j'aurai déjà 10 ans » dit le jeune Mathis. Quel jour de l'année Mathis fête-t-il son anniversaire ?
6 – Suite
Le premier terme d'une suite est 718. Chaque terme suivant est égal à la somme des chiffres du terme précédent multipliée par 13. Quel est le deux mille dix-huitième terme de cette suite ?
7 – Le livre de Mathilde
Mathilde a reçu pour son anniversaire un livre ayant deux cent vingt-cinq pages qui compte trois chapitres. La somme des chiffres des numéros des deux premières pages du deuxième chapitre est égale à 18.
Par un curieux hasard, la somme des chiffres des numéros de deux dernières pages de ce même deuxième chapitre (qui compte plus de deux pages) est aussi égale à 18. Quel est le nombre des pages du deuxième chapitre de ce livre ?
8 – Les triminos
Un trimino est un assemblage de trois petits carrés. On pose des triminos rectangulaires sur une grille carrée de quatre cases sur quatre (sur la figure, un premier trimino est posé). Chaque trimino doit recouvrir exactement trois carrés de la grille dont au moins un carré vide. Il peut donc éventuellement recouvrir d'une case ou de deux cases un trimino déjà posé. Au total, combien de triminos rectangulaires peut-on poser, au maximum, en respectant cette règle ?
9 – Le club de basket
Dans ce club de basket, il y avait exactement 40% de garçons. Six nouveaux garçons se sont inscrits et il y a maintenant autant de garçons que de filles. Combien ce club compte-t-il maintenant d'inscrits (filles et garçons) ?
10 – Loterie
Dans une loterie, on a vendu dix mille billets, numérotés de 0000 à 9999. Le tirage au sort se fait de la manière suivante :
• on tire au sort un nombre à trois chiffres ;
• tous les billets dont le numéro contient tous les chiffres du nombre tiré sont gagnants.
On a tiré au sort le nombre 116. Les billets gagnants seront donc tous les billets contenant au moins deux 1 et au moins un 6, et seulement ceux-là. Combien y aura-t- il de gagnants ?
11 – Le bateau
Un bateau, après avoir effectué la moitié de son trajet, a augmenté sa vitesse de 25 % en raison de la menace d'une tempête. Il est alors arrivé au port une demi-heure plus tôt que prévu. Combien de temps ce bateau a navigué ?
12 – Course automobile
Deux automobilistes sont partis simultanément, l'un d'Arithméville vers Géocity, et l'autre de Géocity vers Arithméville, ces deux villes étant éloignées de 200 km. Ils ont roulé à des vitesses constantes s'exprimant par des nombres entiers de km / h dont la différence est un multiple de 7. Après deux heures de déplacement, la distance entre la voiture la plus rapide et Géocity était cinq fois plus petite que celle entre la voiture la plus lente et Arithméville. Quelle est la vitesse de la voiture la plus rapide ?
13 – Un multiple singulier
Quel est le plus petit multiple de 2 018 dont l'écriture décimale commence par 1111… ? Répondez 0 si vous pensez qu'un tel multiple n'existe pas.
14 – Le petit bois
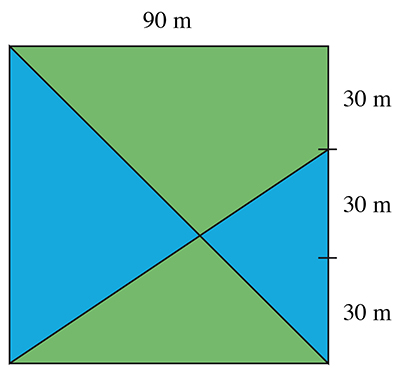
Le petit bois derrière chez moi est un carré de 90 m de côté. Deux allées le traversent : l'une selon une diagonale du carré, l'autre joignant un sommet à un point situé aux deux tiers d'un côté, comme l'indique la figure. Ces deux allées partagent le bois en quatre parcelles. Quelle est l'aire de la plus grande de ces quatre parcelles ?
On donnera la réponse en mètres carrés et on arrondira éventuellement au m2 le plus proche.
15 – La pyramide de Mick Erinos
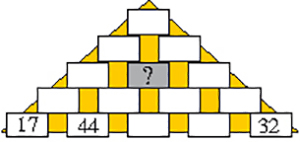
Dans la pyramide de Mick Erinos, chaque brique contient un nombre entier positif et, à partir du premier étage, un nombre égal à la somme des deux nombres inscrits dans les briques sur lesquelles elle est posée. La somme de tous les nombres inscrits dans la pyramide vaut 2 018. Quel est le nombre écrit dans la brique grise ?
16 – Le terrain du Père Fide
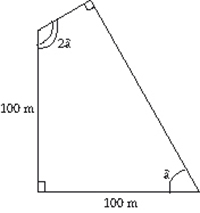Le père Fide possède un terrain quadrilatéral. Ce terrain possède deux côtés perpendiculaires de 100 m de long, deux angles opposés droits et deux autres angles dont l'un mesure le double de l'autre. Quelle est l'aire du terrain du Père Fide ?
On donnera la réponse en mètres carrés et on arrondira éventuellement au m2 le plus proche.
17 – Successeur et double
Le nombre 2 018 est le double d'un nombre premier, 1 009, et le successeur d'un autre nombre premier, 2 017. Quelle sera la prochaine année dont le numéro sera à la fois double et successeur d'un nombre premier ?
18 – Somme des cubes
Mathias adore jouer avec les nombres. Il choisit un premier nombre, calcule la somme des cubes de ses chiffres et écrit le résultat qui sera son deuxième nombre. Il recommence ensuite avec ce deuxième nombre, puis recommence encore et encore jusqu'à ce qu'il tombe sur un nombre déjà écrit. Ainsi, s'il part de 1 012, il écrit 1 012 ; 10 ; 1 ; 1 et il s'arrête. Quel est le plus petit nombre supérieur à 2 018 qui lui permettra de s'arrêter sur le nombre 1 ?