Si A, B et C sont trois points distincts d'un cercle, l'angle  (en bleu) est inscrit dans le cercle. On dit aussi que cet angle intercepte le cercle selon l'arc . Si O est le centre du cercle, l'angle  (en rouge) est l'angle au centre interceptant le même arc  .

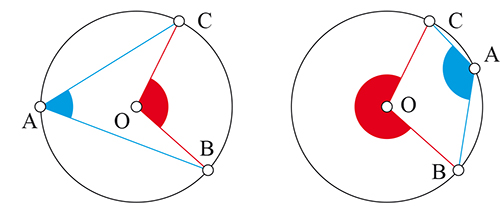
Les deux cas de figures selon que l'angle inscrit est aigu ou obtus.

Du théorème de l'angle au centre au théorème de l'angle inscrit 

Le résultat important dans ce domaine est le théorème de l'angle inscrit. Il possède deux versions, selon que l'on utilise les angles géométriques ou les angles orientés. Commençons par la version classique, qui utilise la définition de l'angle au centre ci-dessus :

Si l'angle  intercepte le même arc   que l'angle au centre  alors   est égal au double de .

Pour le démontrer, on n'a besoin que de deux résultats très simples de géométrie euclidienne : la somme des angles d'un triangle est égale à 180° et les angles à la base d'un triangle isocèle sont égaux. On commence par le cas particulier où l'un des côtés de l'angle ... Lire la suite