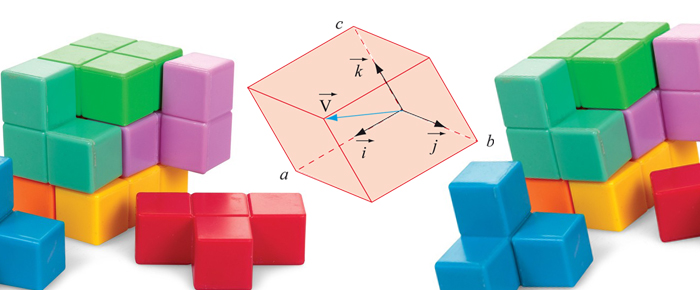
Les triplets de nombres réels se retrouvent dans le paysage des trinômes du second degré, où on ne les attendait pas forcément. Pour s'en convaincre, donnons-nous un polynôme P(x) = a x2 + b x + c. Ce dernier est entièrement défini par les coefficients a, b et c, qui forment donc un triplet de l'espace. L'addition de deux trinômes correspond à l'addition des triplets. De même, la multiplication d'un trinôme P par un scalaire coïncide avec la multiplication du trinôme représentant P par ce scalaire. Autrement dit, l'espace des trinômes du second degré et l'espace usuel sont isomorphes. Il est ainsi possible d'associer à la base = {(1, 0, 0), (0, 1, 0), (0, 0, 1)} de l'espace une base {I, J, K} de l'espace des trinômes : I est le polynôme qui à x associe x2, soit I(x) = x2 ; de même, J(x) = x et K(x) = 1. Ceci permet d'écrire formellement P = a I + b J + c K, ce qui est analogue à l'écriture
Même si on ne peut pas donner à cette décomposition de P le même sens géométrique, elle garde son sens algébrique ... Lire la suite
