
Lorsque vous tenez votre Tangente en main, il n’a que deux dimensions. Il n’y a pourtant aucun problème pour y admirer des images de volumes qui ont trois dimensions. Ces dessins sont toujours des projections et dans la plupart des cas, comme les photos, on a affaire à une projection centrale, dans laquelle on retrouve les lois de la perspective linéaire, connues depuis la Renaissance. Albrecht Dürer en donne une démonstration dans une gravure qui date de 1525.

Sphère et plan
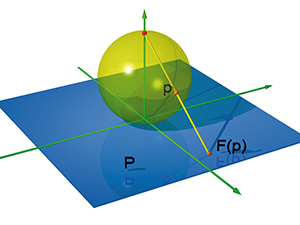 Dans le dessin technique, on utilise souvent la projection orthogonale. L’information d’un objet 3D est exprimé en trois coordonnées (x, y, z), mais on dessine selon deux coordonnées seulement, par exemple (x, y), et on oublie la troisième. Comme on a perdu une partie de l’information, on a besoin de plusieurs dessins (vue de face, vue de côté…). Pour ne pas perdre de l’information, on doit donc choisir une projection qui prend en compte les trois coordonnées d’un objet. C’est le cas pour la projection centrale, mais aussi pour la projection stéréographique. On peut utiliser cette dernière transformation lorsque ce qui nous intéresse se trouve sur une sphère. Sa définition est élémentaire. On considère le plan ... Lire la suite
Dans le dessin technique, on utilise souvent la projection orthogonale. L’information d’un objet 3D est exprimé en trois coordonnées (x, y, z), mais on dessine selon deux coordonnées seulement, par exemple (x, y), et on oublie la troisième. Comme on a perdu une partie de l’information, on a besoin de plusieurs dessins (vue de face, vue de côté…). Pour ne pas perdre de l’information, on doit donc choisir une projection qui prend en compte les trois coordonnées d’un objet. C’est le cas pour la projection centrale, mais aussi pour la projection stéréographique. On peut utiliser cette dernière transformation lorsque ce qui nous intéresse se trouve sur une sphère. Sa définition est élémentaire. On considère le plan ... Lire la suite
