
Si une expression très actuelle sauve ce cube de la platitude absolue,
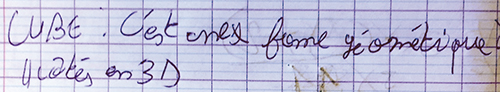
celle-ci,

matière et style dépouillés, laisse cependant planer une relative ambiguïté sur peut-être quelque épaisseur.
Mais pour cet élève, plus d’espoir : cube et cône aplatis d’un seul coup.

Et alors, justement, les cônes ?
À part celui qui plus haut subit le même sort que son infortuné voisin, revoici notre beau parleur :

Un dessin valant mieux qu’une phrase, en voici un, 
semblant plus tenir de la crème glacée que de quelque « solide » rarement proposé en situation d’équilibre aussi précaire. Mais pourquoi pas ?
Certains font des rapprochements bienvenus,

d’autres sont désolés de n’en point trouver.
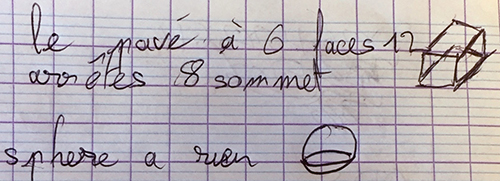
Question posée, en cinquième et en désespoir de définition, à partir de deux dessins, rectangle, et parallélépipède rectangle. « Mais enfin, tu ne vois pas de différence entre les deux ? » « Oui. » « Ah, tout de même ! Et laquelle ? » « Le rectangle, il a pas de pointillés. »
