
« Alice se mit à rire. “Inutile d’essayer, répondit-elle : on ne peut absolument pas croire des choses impossibles.
– Je suppose que tu manques d’entraînement, répondit la Reine. Quand j’avais ton âge, je m’y exerçais une demi-heure par jour. Il m’est arrivé quelquefois de croire jusqu’à six choses impossibles avant le petit déjeuner. Voilà mon châle qui s’en va de nouveau !” »
Lewis Carroll, De l’autre côté du miroir, 1871
Parmi les innombrables énigmes et paradoxes, le classique suivant est sans doute le plus impossible à croire. On vous donne un échiquier sans couleurs, constitué de soixante-quatre carrés et divisé selon les lignes épaisses représentées ci-contre. Il s’agit de reconstituer les quatre pièces en rectangle.
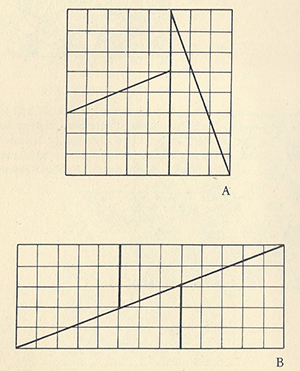
Un compte rapide des petits carrés, de côté et d’autre du rectangle, donne 5 et 13. La surface se constitue donc forcément de soixante-cinq carrés, ce que l’on peut vérifier en comptant individuellement les carrés. D’où est venu le carré supplémentaire ?
Un interstice invisible à l’œil nu
Si l’échiquier est construit avec précision, le rectangle va finalement ne pas posséder une diagonale précise : il va subsister un interstice, que l’épaisseur du trait de crayon va masquer et qui va donc passer inaperçu. La surface de l’espace emprisonné « le ... Lire la suite
