
Sous leurs dehors ludiques voire infantiles, les questions de coloriage dans le plan posent en fait de redoutables défis aux mathématiciens et aux informaticiens. Il a en effet fallu attendre plus de cent ans pour que l’on puisse affirmer que toute carte plane découpée en régions connexes peut être coloriée à l’aide de quatre couleurs de sorte que deux régions limitrophes reçoivent toujours deux couleurs distinctes. C’est le fameux théorème des quatre couleurs, qui avait été avancé dès 1852 et dont la démonstration en 1976 par Kenneth Appel et Wolfgang Haken nécessitait un traitement informatique lourd et ne faisait donc pas consensus. Une nouvelle preuve, formelle cette fois (mais utilisant toujours l’ordinateur de manière cruciale), a été publiée en 2005 par Georges Gonthier et Benjamin Werner ; cette démonstration est aujourd’hui bien mieux acceptée par la communauté. Mais si quatre couleurs suffisent, elles ne sont nullement nécessaires… Dès lors, certaines cartes vont pouvoir être coloriées avec trois couleurs, voire avec seulement deux.
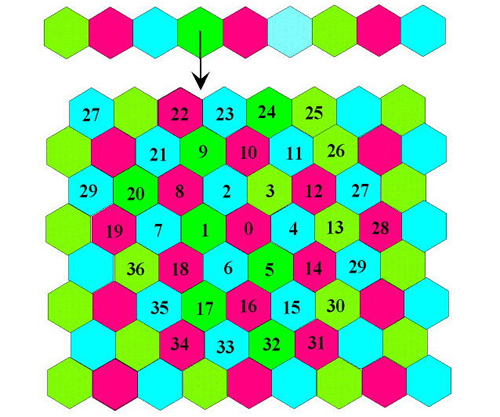
Confection rapide d’un plan pavé d’hexagones.
Des maths en enfilant des perles
Deux couleurs peuvent suffire pour confectionner un collier ouvert, sans que deux perles de même couleur soient en contact. Il suffit d’alterner les couleurs… Maintenant, fermons ce segment de perles colorées sur lui-même. Pour respecter la contrainte, la couleur du début du segment de collier doit être différente de la couleur de fin. Ainsi, le nombre de perles utilisées doit nécessairement être pair. Si la longueur du collier admet un nombre impair de perles, il devient nécessaire de disposer d’une troisième couleur…
Revenons maintenant à une carte dessinée dans le plan, ou à un pavage. Comme pour un vitrail, deux régions sont supposées voisines si elles possèdent une frontière commune (une ligne qui n’est pas réduite à un point).
On distingue essentiellement les pavages réguliers, composés de cellules identiques ou isométriques (quadrilatères, hexagones…), et les pavages irréguliers, composés de cellules non isométriques, avec en outre parfois des lacunes (absences de contact). Pour colorier les pavages réguliers, trois couleurs suffisent, parfois deux. Ainsi, pour colorier un pavage hexagonal régulier (en « nid d’abeilles »), il suffit d’empiler en alternance des segments suivant des « lignes » ordonnées colorées en bleu, vert et rouge. Ce pavage n’est pas modifiable sans provoquer des irrégularités, ce qui n’est pas le cas du plan pavé par des quadrilatères.
Isolons dans ce pavage un groupe de cellules structurées autour d’un élément central, le pivot, entouré d’une couronne (on retrouve ici notre collier de départ) composée d’un nombre pair de cellules (repérées de 1 à 6), alternativement vertes et bleues. Ce groupe prouve que trois couleurs sont bien nécessaires.
.jpg)
Un groupe de cellules, avec pour centre un pivot, 0 (en rouge).
On leur associe naturellement un graphe.
La représentation d’un pavage par un graphe possède l’avantage de représenter les relations de contiguïté des cellules sans se soucier de leur géométrie. Chaque sommet du graphe est une cellule (avec sa couleur) et chaque arête matérialise une frontière du pavage. Cette représentation assure que les propriétés du regroupement précédent (pivot et couronne) s’appliquent à l’ensemble du pavage régulier tout entier. La superposition du regroupement considéré avec tous les autres pivots du pavage illustre en effet que les couleurs des couronnes sont en correspondance : les caractéristiques locales du regroupement comprenant les pavés numérotés de 0 à 6 s’étendent à l’ensemble du plan.
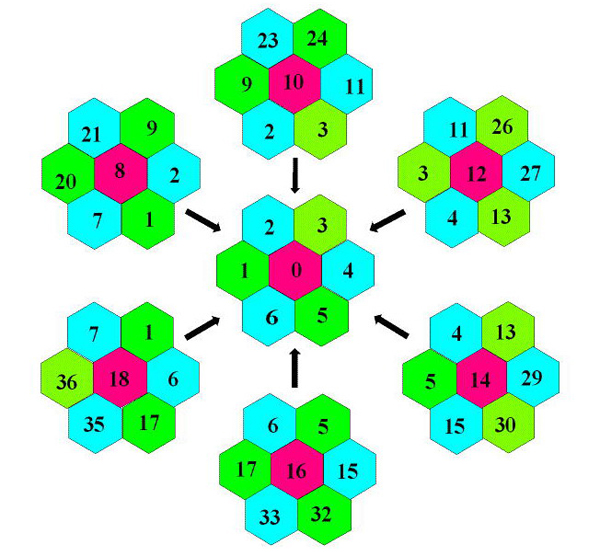
Passage du local au global.
Dans le pavage initial, tous les pivots sont colorés en rouge. Les cellules en vert et en bleu composent les couronnes, se trouvent dans les mêmes positions horaires et participent aux regroupements adjacents.
Dites-le avec des quadrilatères
Comme pour la structure en nid d’abeilles, on peut construire un pavage régulier du plan avec des quadrilatères : il suffit d’empiler en alternance des suites de segments suivant des « lignes » ordonnées colorées en bleu, vert et rouge, par retournement ou par décalage. Ce pavage peut être décliné en deux organisations différentes.
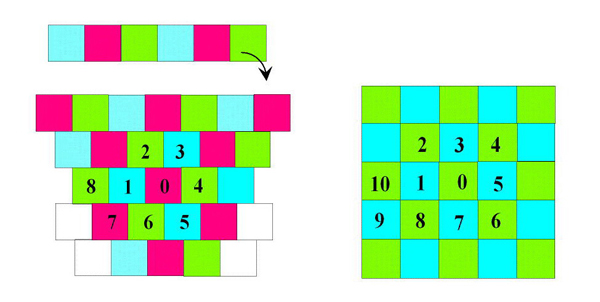
Première configuration à gauche, Seconde configuration à droite.
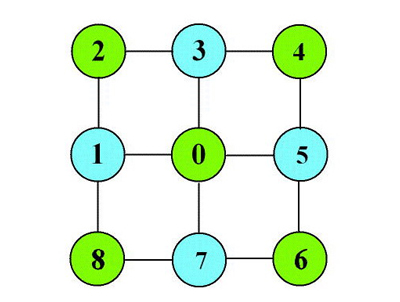
Le graphe associé.
Le premier cas est identique au réseau hexagonal : une couronne de six pavés entoure le pivot. Cette couronne comprend six cellules (un nombre pair), ce qui fournit au total trois couleurs différentes. Dans le second cas, deux couleurs seulement sont nécessaires pour le coloriage. La couronne est certes composée de huit cellules (un nombre pair également), mais ici le pivot peut être muni d’une couleur compatible avec les contraintes.
Lorsque les éléments du plan ne sont plus isométriques, la régularité du coloriage du plan est mise à mal. Pour colorier le plan de la figure ci-dessous, il suffit de choisir un groupe de cellules avec son pivot. Par exemple, la couronne autour de la cellule 0 contient sept cellules. Puisque leur nombre est impair, il sera nécessaire d’utiliser quatre couleurs pour colorier cette première sélection. Prenons pour le pivot 0 la couleur rouge, puis le bleu pour les cellules 1, 3 et 5, alternativement avec le vert pour les cellules 2, 4 et 6. Mais comme les cellules 7 et 1 sont voisines, il faut proposer une nouvelle couleur (le jaune) dans la palette pour achever le coloriage de ce groupe.
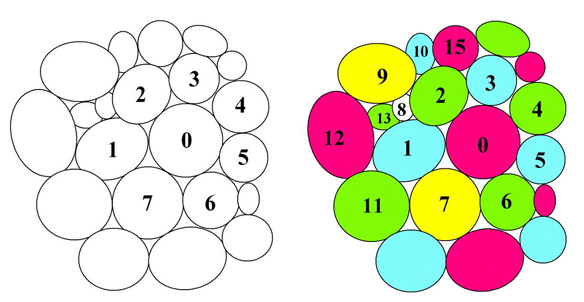
Afin de poursuivre le coloriage, sélectionnons des cellules adjacentes au premier groupe. Par exemple, on choisira la cellule 1 (en bleu) comme pivot du nouveau regroupement. Les cellules qui appartiennent à la nouvelle couronne sont celles numérotées 2, 0 et 7. Pour terminer la couronne, il suffit de prendre les trois cellules suivantes qui sont, chacune, en contact avec le nouveau pivot bleu : 11, 12, 13 et 8 (à colorier en rouge). Cette couronne, maintenant complète, possède un nombre de cellules impair ; elle empruntera une couleur (le jaune) au regroupement précédent.
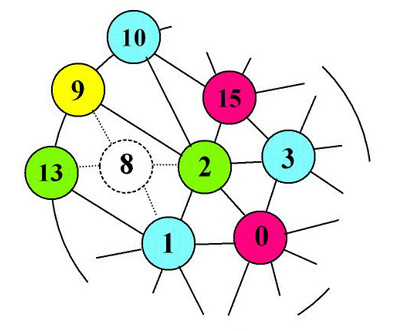
Et si la carte présente des « trous », des régions lacunaires ? L’absence de cellule dans un pavage irrégulier est similaire au cas du pavage à deux couleurs. La couronne se poursuit au-delà du lien manquant. Cette lacune est représentée sur le schéma précédent par la cellule 8, non colorée. Le graphe suivant montre les conséquences.
Une lacune dans le pavage
Si la cellule 8 n’existe pas, alors on se trouve en présence d’une lacune autour du pivot 2. La couronne est alors composée des cellules 1, 13, 9, 10, 15, 3 et 0.
Si 8 est bien présente, la couronne évite la cellule 13 et se raccorde par 1, 8 et 9. La couleur de la cellule 8 sera rouge afin de conserver une palette minimale de couleurs. Le théorème des quatre couleurs nous assure de toute manière qu’un tel coloriage est possible…
