Isaac Newton.
Certainement l’une des plus grandes figures scientifiques de tous les temps. Son œuvre maîtresse, Philosophiæ Naturalis Principia Mathematica, paraît en 1687. Dans ce livre de cinq cent cinquante pages en latin dans lequel il publie enfin des idées parfois développées vingt années plus tôt, il fonde rien de moins que la mécanique classique, révélant les forces de gravitation et les lois universelles du mouvement, qu’il modélise par des équations mathématiques, et jette les bases du calcul différentiel, permettant d’énoncer le principe fondamental de la dynamique, enseigné de nos jours dans tous les lycées. Il faudra cependant attendre le siècle des Lumières et la fin de nombreuses controverses pour voir s’imposer les idées révolutionnaires de Newton.
De la pomme à la gravitation
Selon la légende (rapportée par le biographe et ami de Newton, William Stukeley, d’après une discussion qu’ils ont eue en 1726), c’est vers 1666 que le savant britannique, alors âgé de 24 ans, voyant tomber une pomme dans le jardin de sa mère à Woolsthorpe-by-Colsterworth en Angleterre, a une intuition géniale : la force d’attraction qui fait tomber la pomme est la même que celle qui maintient la Lune en orbite autour de la Terre ! La théorie de la gravitation universelle est en train de naître. Se lançant dans des calculs numériques, Newton vérifie que son intuition correspond aux observations antérieures de Galilée et de Kepler. Il postule ce que nous appelons aujourd’hui les lois de Newton. Par un tour de force mathématique, il parvient à déduire de ce postulat que les planètes suivent des trajectoires elliptiques. Il retrouve ainsi les lois de Kepler. C’est ainsi que, en parallèle des travaux de Leibniz, qui en est considéré comme le co-fondateur, le calcul infinitésimal est en train de naître également, préfigurant les notions de limite et de dérivée qui seront formalisées plus tard par Augustin Louis Cauchy, Leonhard Euler, Karl Weierstrass…
Quelle attitude remarquable que celle de Newton qui, partant d’observations et de données numériques, en tire un modèle abstrait, l’analyse pour confirmer les observations, puis l’extrapole, obtenant ainsi une compréhension fine d’un phénomène naturel ! Les Principia Mathematica marquent certainement le début de la mathématisation des sciences et de ce qui est la démarche scientifique générale en mathématiques : observer, modéliser, analyser, simuler, dans le but de prévoir, d’optimiser et de contrôler. Pour la première fois est réellement mise en pratique la pensée de Galilée : « La nature est un livre écrit en langage mathématique. »
L’approche scientifique de Newton est en effet étonnamment moderne : il n’accepte que les relations mathématiques découvertes par l’observation rigoureuse des phénomènes. « Hypotheses non fingo », aime-t-il à répéter (« Je ne feins pas d’hypothèses »).
Ainsi, vers 1666, Newton veut confronter à l’expérience la loi de gravitation qu’il vient de postuler. Malheureusement, les estimations connues à cette époque de la distance Terre–Lune et du rayon terrestre sont trop grossières, et avec les données dont il dispose, il trouve que notre satellite devrait tomber sur la Terre ! Devant cette divergence, il renonce (provisoirement) à sa théorie. C’est seulement seize ans plus tard, en 1682, qu’il apprend à la Royal Society de Londres qu’une valeur beaucoup plus précise du rayon terrestre vient d’être déterminée par le Français Jean-Félix Picard (dit l’abbé Picard, 1620–1682). Avec cette valeur, Newton trouve que sa théorie est finalement conforme avec les observations !
On est alors dans la genèse des Principia Mathematica. À cette époque, le monde scientifique est en ébullition, et l’idée d’une force d’attraction qui soit inversement proportionnelle au carré de la distance entre deux corps est dans l’air du temps, notamment avec les travaux d’Edmond Halley (1656–1742) ou de Robert Hooke (1635–1703). Hooke avait clairement formulé le caractère universel d’une force d’attraction gravitationnelle, mais il ne possédait pas le génie mathématique de Newton qui lui aurait permis de formaliser rigoureusement ses idées et de retrouver les lois de Kepler, notamment le fait que les planètes suivent des trajectoires elliptiques. Les deux compatriotes vont beaucoup correspondre, et aussi s’opposer de manière virulente…
Newton, qui occupe une chaire à Cambridge, a repris les travaux de Halley sur la mécanique céleste en 1677. En 1684, le jeune astronome qui donnera son nom à une fameuse comète demande à Newton quelle trajectoire suivrait un corps soumis à une force inversement proportionnelle à la distance. Ce dernier lui répond immédiatement que c’est une ellipse, comme il l’a calculé vingt ans plus tôt sans l’avoir publié. Il fait parvenir au jeune astronome quelques pages démontrant ce fait. Impressionné, son correspondant l’encourage à publier et le finance partiellement.
Le retour de la comète
Les Principia Mathematica paraissent enfin en 1687. Newton accède alors à une grande reconnaissance internationale. En France, sa reconnaissance sera plus tardive car c’est la théorie des tourbillons de Descartes qui prévaut, théorie selon laquelle les planètes se déplacent dans une sorte d’éther qui maintient les planètes sur leur orbite… Des controverses s’installent d’ailleurs entre newtoniens d’un côté et cartésiens de l’autre. C’est seulement vers 1750 que, notamment grâce aux efforts de Pierre Louis Moreau de Maupertuis, Alexis Clairaut, Voltaire, Émilie du Châtelet et grâce à l’Encyclopédie de Diderot et D’Alembert, la mécanique newtonienne sera enfin adoptée dans notre pays. En 1759, le retour de la comète de Halley, prévu par les théories de Newton, assure leur triomphe définitif.
La compréhension des lois de Newton permet alors de poser dans un cadre mathématique le célèbre problème des N corps, qui consiste à résoudre les équations différentielles régissant le mouvement de corps qui interagissent gravitationnellement. C’est un problème fondamental en mathématiques et en astronomie, que Newton a cherché à résoudre (sans succès) lorsque N = 3. Un siècle plus tard, dans la continuité de travaux d’Euler, Joseph-Louis Lagrange étudie le problème des trois corps restreint, dans lequel deux corps sont « très massifs » (par exemple, le Soleil et la Terre) et le troisième est de masse « négligeable » par rapport aux deux autres (comme une pierre, un astéroïde, un engin spatial). Il démontre que la dynamique de Newton, dans un repère tournant, admet cinq points d’équilibre, que l’on appelle désormais les points de Lagrange.
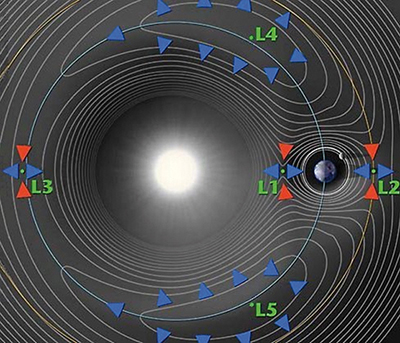
La propriété d’être un point d’équilibre est intéressante : elle offre la possibilité d’avoir une configuration fixe relativement à deux corps célestes et permet donc de concevoir des sites d’observation spatiale. En effet, si l’on place un objet exactement en un point de Lagrange, alors (en théorie du moins…) il y reste !
On dit bien « en théorie », car alors se pose la question de la stabilité locale de ces points d’équilibre. Comme sur la figure, où sont représentées des orbites (trajectoires possibles d’une pierre dans le système Soleil–Terre), il s’avère que les points L1, L2 et L3 sont naturellement instables, alors que les points L4 et L5 sont stables. Cela signifie que, en pratique, si l’on place un caillou au voisinage de l’un des points L4 ou L5, alors le caillou va se mettre à dériver mais va rester dans un tel voisinage. Au contraire, si on le place juste à côté de l’un des points L1, L2 ou L3, alors il ne restera pas dans leur voisinage.
« En théorie », si le caillou est placé exactement au point L1, alors il ne bouge pas. Mais dans la pratique, la moindre perturbation (vent solaire, perturbations dues à d’autres corps célestes…) lui fera quitter le point L1, et donc dériver à plus ou moins long terme. La situation est similaire à celle d’un bâton que l’on poserait sur une table : lorsqu’il est exactement vertical, il reste dans sa position, mais cet équilibre est instable. À la moindre perturbation, il tombe.
Tenir un bâton dans la main
Au premier abord, la propriété de stabilité autour de L4 et L5 peut sembler être une bonne nouvelle : si l’on place un engin spatial au voisinage de l’un de ces points, il va y rester. Mais, en fait, autour de ces points gravitent quantité de poussières ou de petits corps célestes qui se sont retrouvés « piégés » dans ce puits de potentiel qui, comme une cuvette, au fur et à mesure des hasards astronomiques, a retenu ces astéroïdes (dont les fameux astéroïdes troyens dans le système Soleil–Jupiter), rendant ainsi impossible la présence d’un engin spatial dans cette zone à cause des inévitables chocs qui l’abîmeraient rapidement.
L’instabilité des points L1, L2 et L3 est donc finalement, en un certain sens, une bonne nouvelle : ce sont des sites « naturellement propres » ! Mais pour garder l’objet au voisinage de ces points de Lagrange, il est nécessaire de faire appel à la théorie mathématique du contrôle, et en particulier de la stabilisation. Reprenons l’exemple du bâton, que l’on essaie maintenant de maintenir en équilibre vertical sur un doigt ou dans le creux de la main, quitte à devoir bouger un peu. L’équilibre vertical étant instable, la stabilisation consiste ici à s’autoriser à bouger légèrement la main (on fait du contrôle) de manière à compenser de faibles variations autour de l’équilibre, et ainsi maintenir le bâton autour de son équilibre instable. Dans le cas d’un engin spatial au voisinage d’un point de Lagrange instable, l’idée est qu’une légère propulsion (fournie par exemple par des panneaux solaires) suffit à le maintenir dans la zone d’intérêt. Cela ne requiert que peu d’énergie.
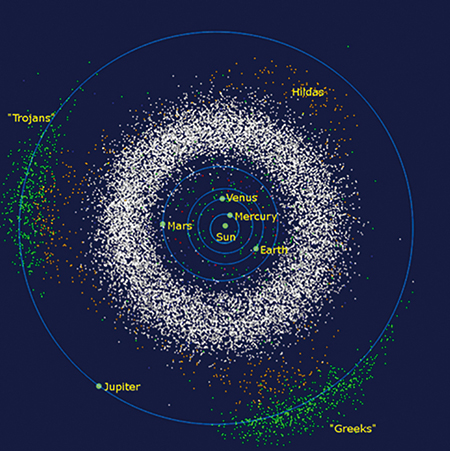
Dans le système Soleil–Jupiter, les astéroïdes troyens se situent au voisinage du point de Lagrange L5.
Les points de Lagrange L1 et L2 du système Soleil–Terre sont utilisés depuis longtemps par les agences spatiales, qui y placent de nombreux engins. Par exemple, autour du point L1 (qui se situe à environ 1,5 million de kilomètres de la Terre dans la direction du Soleil) gravite depuis 1996 le satellite SOHO, dont la mission est d’observer la surface de notre astre, ses taches, les éruptions solaires… Autour du point L2 sera lancé (en principe en 2020) le successeur du télescope Hubble, appelé JWST (James Webb Space Telescope), dont la position sera idéale puisqu’il ne sera pas gêné par la lumière solaire.
Des trajectoires périodiques
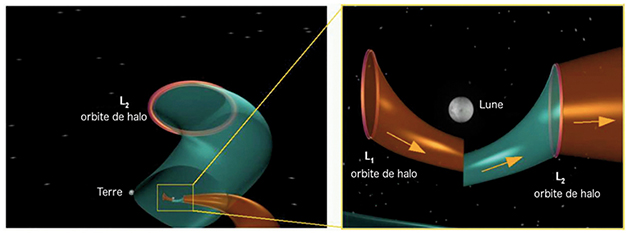
En utilisant des théorèmes d’Alexandre Lyapunov, d’Henri Poincaré, puis la théorie des systèmes dynamiques développée dans les années 1960, les mathématiques ont permis de découvrir autour des points de Lagrange des propriétés insoupçonnées du champ gravitationnel newtonien, remarquablement utiles pour l’élaboration de missions spatiales : il existe autour de chaque point de Lagrange une multitude de trajectoires périodiques et quasi périodiques, les plus connues étant les orbites de halo (qui sont des déformations de cercles). On y trouve aussi toutes les orbites possibles de Lissajous. Ces propriétés surprenantes sont dues à la complexité du champ gravitationnel dans le problème à plusieurs corps. Les trajectoires correspondantes sont intéressantes car on peut stabiliser un engin spatial le long de telles orbites avec un coût énergétique très faible.
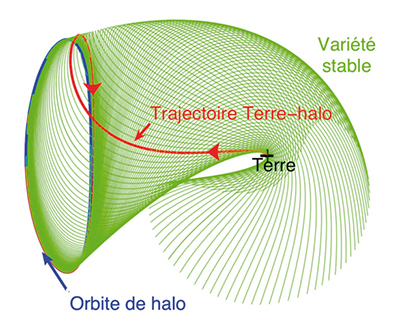
Variété stable invariante (en vert) générée par une orbite de halo.
Le point le plus fascinant reste que chacune de ces orbites périodiques engendre des variétés (stables ou instables) invariantes. Ce sont des sortes de tubes s’appuyant sur l’orbite périodique qui les engendre, et qui se comportent en véritables « courants de gravité », similaires à des courants marins : si l’on dépose un caillou à l’intérieur d’un tel « tube », alors il va se mettre à dériver (assez lentement) selon le courant, en restant à l’intérieur du tube. On peut donc en profiter pour se déplacer, de manière totalement gratuite et parfaitement calculable, donc prédictible.
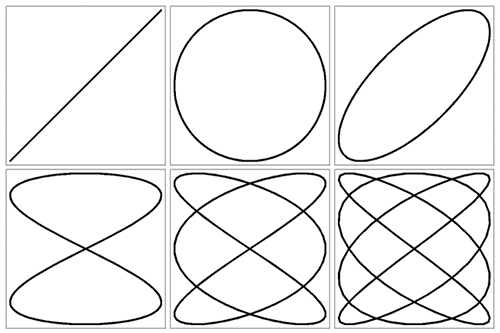
Orbites de halo (en haut) et courbes de Lissajous (en bas).
Des voyages à très bas coût
Vision d’artiste des courants de gravité (tubes invariants).
La cartographie des courants de gravité permet alors d’envisager des missions spatiales interplanétaires qui sont quasi gratuites en termes de consommation d’énergie. Le low cost gagne aussi les missions spatiales interplanétaires ! Toutefois, à l’instar des courants marins, le déplacement le long de tels courants est lent, donc plutôt adapté à des missions robotisées. Ou alors il faut combiner leur effet d’entraînement à l’utilisation d’un moteur…
Par exemple, en utilisant les points de Lagrange L1 et L2 du système Terre–Lune et les courants de gravité qu’ils engendrent, on sait aller de la Terre à la Lune de manière presque « gratuite », à ceci près qu’il faut bien sûr au préalable s’arracher de l’attraction terrestre. Une fois l’engin placé dans un tube invariant, on sait l’emmener à proximité (environ 1 500 km) de la surface de la Lune en trois à quatre mois, sans aucune dépense de carburant ! Dans un avenir proche, la communauté internationale pourrait ainsi s’accorder à construire une base lunaire (sans doute au pôle Nord de la Lune), qui servirait de point intermédiaire en vue de missions vers Mars.
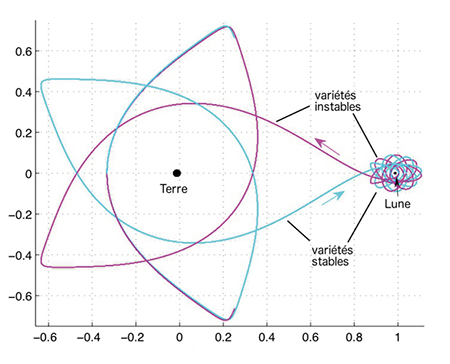
Le cas du système Terre–Lune.
De manière plus prospective, on sait concevoir des missions interplanétaires lointaines, permettant d’aller visiter « à très bas coût » les satellites de Jupiter ou de Saturne. Le prix à payer toutefois est le temps de parcours… Des missions humaines lointaines ne pourront donc pas se contenter d’utiliser ce réseau de courants de gravité, mais on peut envoyer des robots, qui seront alors capables d’aller explorer les confins du système solaire, et peut-être au-delà.
.jpg)
Ce texte est issu de la conférence donnée par Emmanuel Trélat le mercredi 23 janvier 2019 à la Bibliothèque nationale de France dans le cadre du cycle « Un texte, un mathématicien ».
Emmanuel Trélat est professeur à Sorbonne Université (Paris-VI) et dirige la Fondation Sciences mathématiques de Paris. Il a été récompensé par de nombreux prix, notamment pour avoir conçu le logiciel désormais utilisé pour les lanceurs Ariane.