Les transformations géométriques du plan ou de l’espace que l’on considère le plus couramment ont en général la propriété de conserver l’alignement des points, c’est-à-dire que les images de trois points alignés sont également trois points alignés. C’est le cas des rotations, des translations, mais aussi des projections orthogonales sur une droite ou sur un plan.
Ces transformations conservent également le rapport des longueurs, c’est-à-dire que si deux segments pris sur une même droite D sont tels que l’un est deux fois plus long que l’autre, il en est de même de leurs images sur la droite D’ image de D.
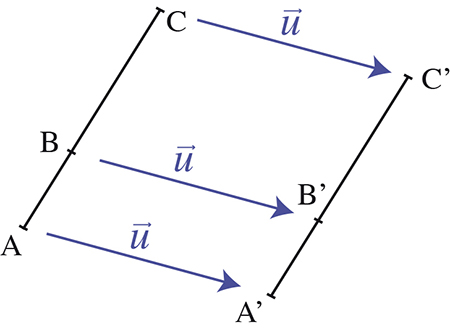
La translation de vecteur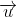 
conserve l’alignement des points A, B et C, ainsi que la position relative de B dans le segment [AC].
L’apport des artistes
Les peintres de la Renaissance, pour représenter la profondeur, se sont intéressés à la projection de l’espace sur le plan de la toile. Cette projection est issue d’un point, l’œil. Mathématiquement, c’est ce que l’on nomme une projection centrale (voir FOCUS). Certes, celle-ci conserve l’alignement ; en revanche, ce n’est plus le cas de la proportionnalité.
On sait depuis le mathématicien allemand Felix Klein (1849–1925) combien la géométrie est friande de ...
Lire la suite